如图，某小区有一块平行四边形的花坛，分别种有红、黄、蓝、绿、橙、紫6种颜色的花．如果有AB∥EF∥DC，BC∥GH∥AD，那么下列说法错误的是（ ）
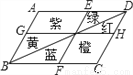
A. 红花、绿花种植面积一定相等 B. 紫花、橙花种植面积一定相等
C. 红花、蓝花种植面积一定相等 D. 蓝花、黄花种植面积一定相等
C
【解析】∵AB∥EF∥DC，BC∥GH∥AD，
∴GH、BD、EF把一个平行四边形分割成四个小平行四边形，
∴一条对角线可以把一个平行四变形的面积一分为二，
据此可从图中获得S黄=S蓝，S绿=S红，S（紫+黄+绿）=S（橙+红+蓝），
根据等量相减原理知S紫=S橙，
∴A、B、D说法正确，
再考查S红与S蓝显然不相等．
故选C． 已知□ABCD中,AB=8 cm,BC=7 cm,则此平行四边形的周长为_________cm.
30
【解析】平行四边形的周长为（8+7）×2=30cm. 如图，在□ABCD中，∠D＝72°，BE平分∠ABC，则∠ABE的度数是_______．
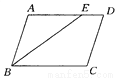
36°
【解析】∵四边形ABCD是平行四边形，
∴∠ABC=∠D=72°.
∵BE平分∠ABC，
∴∠ABE=∠ABC=36°. 平行四边形两邻边长分别为20和16，若两条较长边之间的距离为6，则两条较短边之间的距离为_______．
7.5
【解析】由题意得
20×6÷16=7.5cm. 如图，已知AB∥CD，则x的度数是____________.
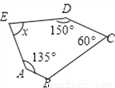
75º
【解析】∵AB∥CD，
∴∠B=180°-60°=120°，
∵多边形ABCDE是五边形，
∴∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°，
∴∠E=540°-∠A-∠B-∠C-∠D=540°-135°-120°-60°-150°=75°． 如图，在四边形ABCD中，P是BC边上一点，∠A=∠B=90º，E为AB的中点，连接DP，EP.若FG为△DPE的中位线，AB=AD=4，则FG=___________.
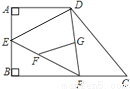
【解析】∵点E是AB的中点，AB=4，
∴AE=AB=2.
∵∠A=90°，
∴DE=.
∵FG是△EDP的中位线，
∴FG=ED=. 如图所示，在□ABCD中，AC与BD相交于点O，AB⊥AC，∠DAC＝45°，AC＝2，则BD的长是_______．
2
【解析】∵四边形ABCD是平行四边形，∠DAC=45°，
∴∠ACB=∠DAC=45°，OA=AC=1，
∵AB⊥AC，
∴△ABC是等腰直角三角形，
∴AB=AC=2，
在Rt△AOB中，根据勾股定理得OB= ，
∴BD=2BO=2. 如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件_________使四边形AECF是平行四边形(只填一个即可).
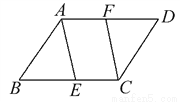
AF=CE（答案不唯一）
【解析】试题分析：添加的条件是AF=CE．理由是：
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴AF∥CE，
∵AF=CE，
∴四边形AECF是平行四边形． 如图，在平行四边形ABCD中，AB=4，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG=1，则AE的边长为（ ）.
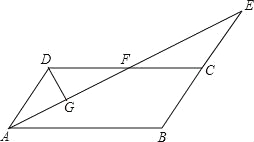
A．2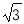
B．4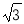
C．4 D．8
B.
【解析】
试题分析：由AE为角平分线，得到一对角相等，再由ABCD为平行四边形，得到AD与BE平行，利用两直线平行内错角相等得到一对角相等，等量代换及等角对等边得到AD=DF，由F为DC中点，AB=CD，求出AD与DF的长，得出三角形ADF为等腰三角形，根据三线合一得到G为AF中点，在直角三角形ADG中，由AD与DG的长，利用勾股定理求出AG的长，进而求出AF的长，再由三角形AD... 一个多边形的内角和与外角和相加正好是一个九边形的内角和，试求这个多边形的边数.
7
【解析】试题分析：设这个多边形的边数为n,根据多边形内角和与外角和定理得出(n－2) ×180º+360º=(9－2)×180º，,解之可得.
【解析】
设这个多边形的边数为n，则根据题意，
得 (n－2)·180º+360º=(9－2)×180º，
解得n=7.
所以这个多边形的边数为7.