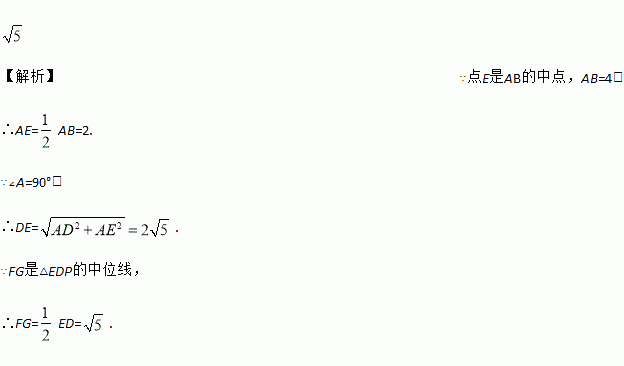题目内容
如图,在四边形ABCD中,P是BC边上一点,∠A=∠B=90º,E为AB的中点,连接DP,EP.若FG为△DPE的中位线,AB=AD=4,则FG=___________.
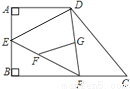
 【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=.
【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
当k=____________时,方程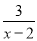 =2-
=2-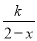 会产生增根.
会产生增根.
 3
【解析】=2-,去分母得: ,当x=2时,k=3.
故答案:3.
3
【解析】=2-,去分母得: ,当x=2时,k=3.
故答案:3. 计算﹣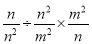 的结果为( )
的结果为( )
A. ﹣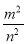 B. ﹣
B. ﹣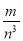 C. ﹣
C. ﹣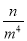 D. ﹣n
D. ﹣n
 A
【解析】【解析】
原式= .故选A.
A
【解析】【解析】
原式= .故选A. 某学校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,求原价每瓶多少元?若设原价每瓶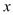 元,则可列出方程为( )
元,则可列出方程为( )
A. 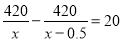 B.
B. 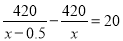
C. 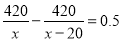 D.
D. 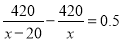
 B
【解析】设原价每瓶x元,根据某校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,可列方程.
【解析】
设原价每瓶x元,
=20.
故选B.
B
【解析】设原价每瓶x元,根据某校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,可列方程.
【解析】
设原价每瓶x元,
=20.
故选B. 如图,在△ABC中,∠BAC=90º,延长BA到点D,使AD=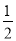 AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
 见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E...
见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E... 如图,某小区有一块平行四边形的花坛,分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( )
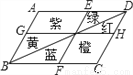
A. 红花、绿花种植面积一定相等 B. 紫花、橙花种植面积一定相等
C. 红花、蓝花种植面积一定相等 D. 蓝花、黄花种植面积一定相等
 C
【解析】∵AB∥EF∥DC,BC∥GH∥AD,
∴GH、BD、EF把一个平行四边形分割成四个小平行四边形,
∴一条对角线可以把一个平行四变形的面积一分为二,
据此可从图中获得S黄=S蓝,S绿=S红,S(紫+黄+绿)=S(橙+红+蓝),
根据等量相减原理知S紫=S橙,
∴A、B、D说法正确,
再考查S红与S蓝显然不相等.
故选C.
C
【解析】∵AB∥EF∥DC,BC∥GH∥AD,
∴GH、BD、EF把一个平行四边形分割成四个小平行四边形,
∴一条对角线可以把一个平行四变形的面积一分为二,
据此可从图中获得S黄=S蓝,S绿=S红,S(紫+黄+绿)=S(橙+红+蓝),
根据等量相减原理知S紫=S橙,
∴A、B、D说法正确,
再考查S红与S蓝显然不相等.
故选C. 如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
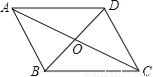
A. 18 B. 28 C. 36 D. 46
 C
【解析】试题分析:由平行四边形的性质和已知条件计算即可,解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体.
【解析】
∵四边形ABCD是平行四边形,
∴AB=CD=5,
∵△OCD的周长为23,
∴OD+OC=23﹣5=18,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=...
C
【解析】试题分析:由平行四边形的性质和已知条件计算即可,解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体.
【解析】
∵四边形ABCD是平行四边形,
∴AB=CD=5,
∵△OCD的周长为23,
∴OD+OC=23﹣5=18,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=... 若分式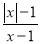 的值为0,则x的值等于___________
的值为0,则x的值等于___________
 -1
【解析】试题分析:因为当时分式的值为零,解得且,所以x=1.
-1
【解析】试题分析:因为当时分式的值为零,解得且,所以x=1. 如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.
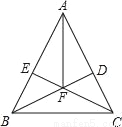
 证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴...
证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴...