题目内容
平行四边形两邻边长分别为20和16,若两条较长边之间的距离为6,则两条较短边之间的距离为_______.
 7.5
【解析】由题意得
20×6÷16=7.5cm.
7.5
【解析】由题意得
20×6÷16=7.5cm.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若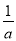 +
+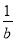 =
=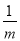 (a≠b≠0),用含a、b的代数式表示m,则m=___________.
(a≠b≠0),用含a、b的代数式表示m,则m=___________.
 【解析】根据+=得, ,得: .
故答案: .
【解析】根据+=得, ,得: .
故答案: . 已知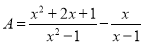 .
.
(1)化简A;
(2)当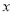 满足不等式组
满足不等式组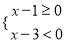 ,且
,且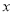 为整数时,求A的值.
为整数时,求A的值.
 (1);(2)1
【解析】试题分析:首先将分式的分子和分母进行因式分解,然后进行约分,最后根据同分母的分式减法法则得出化简的答案;根据题意求出不等式组的整数解,然后根据分式的性质求出x的值,将x的值代入化简后的式子进行计算.
试题解析:(1)原式====
(2)不等式组的解集为1≤x<3 ∵x为整数 ∴x=1或2
∵A=∴x-1≠0 即x≠1 ∴x=2
当x=2时,原...
(1);(2)1
【解析】试题分析:首先将分式的分子和分母进行因式分解,然后进行约分,最后根据同分母的分式减法法则得出化简的答案;根据题意求出不等式组的整数解,然后根据分式的性质求出x的值,将x的值代入化简后的式子进行计算.
试题解析:(1)原式====
(2)不等式组的解集为1≤x<3 ∵x为整数 ∴x=1或2
∵A=∴x-1≠0 即x≠1 ∴x=2
当x=2时,原... 使分式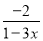 的值为正的条件是( )
的值为正的条件是( )
A. 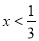 B.
B. 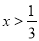 C. x<0 D. x>0
C. x<0 D. x>0
 B
【解析】由题意得
1-3x<0,
解之得
.
故选B.
B
【解析】由题意得
1-3x<0,
解之得
.
故选B. 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( ).
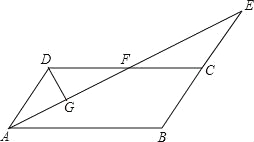
A.2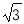 B.4
B.4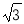 C.4 D.8
C.4 D.8
 B.
【解析】
试题分析:由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形AD...
B.
【解析】
试题分析:由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形AD... 如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
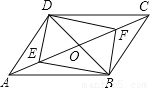
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
 B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B. 一个多边形的内角和与外角和的度数之比为2∶1,则这个多边形的边数为( )
A. 3 B. 4 C. 5 D. 6
 D
【解析】设这个多边形有n条边,由题意得
(n-2) ×180:360=2:1,
解之得
n=6.
故选D.
D
【解析】设这个多边形有n条边,由题意得
(n-2) ×180:360=2:1,
解之得
n=6.
故选D. 分式方程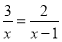 的解是( )
的解是( )
A. 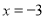 B.
B. 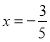 C.
C. 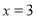 D. 无解
D. 无解
 C.
【解析】
试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
去分母得:3x-3=2x,
解得:x=3,
经检验x=3是分式方程的解.
故选C.
考点: 解分式方程.
C.
【解析】
试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
去分母得:3x-3=2x,
解得:x=3,
经检验x=3是分式方程的解.
故选C.
考点: 解分式方程. △ABC中,若∠A=80°,∠B=50°,AC=5,则AB= .
 5.
【解析】
试题解析:∵∠A=80°,∠B=50°,
∴∠C=180°-80°-50°=50°,
∴AB=AC=5.
5.
【解析】
试题解析:∵∠A=80°,∠B=50°,
∴∠C=180°-80°-50°=50°,
∴AB=AC=5. 
