��Ŀ����
��ͼ��ijС����һ��ƽ���ı��εĻ�̳���ֱ����к졢�ơ������̡��ȡ���6����ɫ�Ļ��������AB��EF��DC��BC��GH��AD����ô����˵��������ǣ� ��
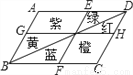
A. �컨���̻���ֲ���һ����� B. �ϻ����Ȼ���ֲ���һ�����
C. �컨��������ֲ���һ����� D. �������ƻ���ֲ���һ�����
 C
����������AB��EF��DC��BC��GH��AD��
��GH��BD��EF��һ��ƽ���ı��ηָ���ĸ�Сƽ���ı��Σ�
��һ���Խ��߿���һ��ƽ���ı��ε����һ��Ϊ����
�ݴ˿ɴ�ͼ�л��S��=S����S��=S�죬S����+��+�̣�=S����+��+������
���ݵ������ԭ��֪S��=S�ȣ�
��A��B��D˵����ȷ��
�ٿ���S����S����Ȼ����ȣ�
��ѡC��
C
����������AB��EF��DC��BC��GH��AD��
��GH��BD��EF��һ��ƽ���ı��ηָ���ĸ�Сƽ���ı��Σ�
��һ���Խ��߿���һ��ƽ���ı��ε����һ��Ϊ����
�ݴ˿ɴ�ͼ�л��S��=S����S��=S�죬S����+��+�̣�=S����+��+������
���ݵ������ԭ��֪S��=S�ȣ�
��A��B��D˵����ȷ��
�ٿ���S����S����Ȼ����ȣ�
��ѡC��
�������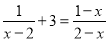 �������� ������_______��
�������� ������_______��
 x=2
����������ԭ������������
�����ĸx-2=0��
���x=2��
�ʴ�Ϊ��x=2.
x=2
����������ԭ������������
�����ĸx-2=0��
���x=2��
�ʴ�Ϊ��x=2. �����з��̣�
��1��1��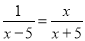 ��2��
��2��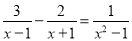 ��
��
 (1) ;(2)x=-5
�������������������ȥ��ĸ���ѷ�ʽ����ת��Ϊ��ʽ���̣�Ȼ������ʽ���̵Ľⷨ��⣬���δ֪����ֵ��Ҫ���.
��������
��1��ȥ��ĸ�ã�x2��25��x��5=x2��5x��
��ã�x=��
������x=�Ƿ�ʽ���̵Ľ⣻
��2��ȥ��ĸ�ã�3x+3��2x+3=1��
��ã�x=��5��
������x=��5�Ƿ�ʽ���̵Ľ⣮
(1) ;(2)x=-5
�������������������ȥ��ĸ���ѷ�ʽ����ת��Ϊ��ʽ���̣�Ȼ������ʽ���̵Ľⷨ��⣬���δ֪����ֵ��Ҫ���.
��������
��1��ȥ��ĸ�ã�x2��25��x��5=x2��5x��
��ã�x=��
������x=�Ƿ�ʽ���̵Ľ⣻
��2��ȥ��ĸ�ã�3x+3��2x+3=1��
��ã�x=��5��
������x=��5�Ƿ�ʽ���̵Ľ⣮ ��ͼ��ʾ����ƽ���ı���ABCD�У��ӳ�DA����E���ӳ�BC����F��ʹ��AE=CF������EF���ֱ�AB��CD�ڵ�M��N������DM��BN��
��1����֤����AEM�ա�CFN��
��2����֤��BD��MN����ƽ�֣�
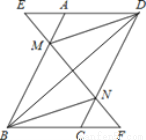
 ��1��֤����������2��֤��������
�������������������1���ȸ���ƽ���ı��ε����ʿɵó�AD��BC����DAB=��BCD���ٸ���ƽ���ߵ����ʼ����ǵ����ʵó���E=��F����EAM=��FCN���Ӷ�����ASA������֤����
��2������ƽ���ı��ε����ʼ�(1)�Ľ��ۿɵ�BM ƽ���ҵ���DN��������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵ��ı���BMDN��ƽ���ı��Σ�����ƽ���ı��ε����ʼ���֤�����ۣ�...
��1��֤����������2��֤��������
�������������������1���ȸ���ƽ���ı��ε����ʿɵó�AD��BC����DAB=��BCD���ٸ���ƽ���ߵ����ʼ����ǵ����ʵó���E=��F����EAM=��FCN���Ӷ�����ASA������֤����
��2������ƽ���ı��ε����ʼ�(1)�Ľ��ۿɵ�BM ƽ���ҵ���DN��������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵ��ı���BMDN��ƽ���ı��Σ�����ƽ���ı��ε����ʼ���֤�����ۣ�... ��ͼ�����ı���ABCD�У�P��BC����һ�㣬��A=��B=90º��EΪAB���е㣬����DP��EP.��FGΪ��DPE����λ�ߣ�AB=AD=4����FG=___________.
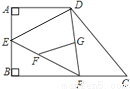
 ���������ߵ�E��AB���е㣬AB=4��
��AE=AB=2.
�ߡ�A=90�㣬
��DE=.
��FG�ǡ�EDP����λ�ߣ�
��FG=ED=.
���������ߵ�E��AB���е㣬AB=4��
��AE=AB=2.
�ߡ�A=90�㣬
��DE=.
��FG�ǡ�EDP����λ�ߣ�
��FG=ED=. ��ͼ��ʾ,�ı���ABCD��,�Խ���AC,BD�ཻ�ڵ�O,�������������ж�����ı�����ƽ���ı��ε��� (����)
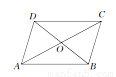
A. AB��DC,AD��BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB��DC,AD=BC
 D
�����������������A����������Ա߷ֱ�ƽ�е��ı���Ϊƽ���ı��Σ�B����������Ա߷ֱ���ȵ��ı���Ϊƽ���ı��Σ�C�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ�D�������ж�.
D
�����������������A����������Ա߷ֱ�ƽ�е��ı���Ϊƽ���ı��Σ�B����������Ա߷ֱ���ȵ��ı���Ϊƽ���ı��Σ�C�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ�D�������ж�. ����һ������ˮ���Ļ����ν��ڼ䣬����ͬѧ����һ�������ǰȥ���Σ�����������Ϊ180Ԫ������ʱ������������ͬѧ�����ÿ��ͬѧ��ԭ����̯��3ԪǮ���ѣ���μ�������ͬѧ��x�ˣ�Ӧ������г����̣���������⣬ֻ�г����ɣ�
 ����������������ԭ���μ�������ͬѧ��x�ˣ�����������Ϊ180Ԫ������ʱ������������ͬѧ�����ÿ��ͬѧ��ԭ����̯��3ԪǮ���ѣ����з��̣�
�����������μ�������ͬѧ��x�ˣ���ô����ǰΪx��2�ˣ�
����������Եó�
����������������ԭ���μ�������ͬѧ��x�ˣ�����������Ϊ180Ԫ������ʱ������������ͬѧ�����ÿ��ͬѧ��ԭ����̯��3ԪǮ���ѣ����з��̣�
�����������μ�������ͬѧ��x�ˣ���ô����ǰΪx��2�ˣ�
����������Եó� �����Ƿ�ʽ���̵��ǣ� ��
A. 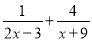 B.
B. 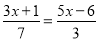
C. 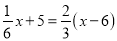 D.
D. 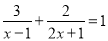
 D
��������A�����Ƿ��̣��ʱ�ѡ�����
B����ĸ�в�����δ֪��������ʽ���̣��ʱ�ѡ�����
C����ĸ�в�����δ֪��������ʽ���̣��ʱ�ѡ�����
D����ĸ�к���δ֪�����Ƿ�ʽ���̣��ʱ�ѡ����ȷ��
��ѡD��
D
��������A�����Ƿ��̣��ʱ�ѡ�����
B����ĸ�в�����δ֪��������ʽ���̣��ʱ�ѡ�����
C����ĸ�в�����δ֪��������ʽ���̣��ʱ�ѡ�����
D����ĸ�к���δ֪�����Ƿ�ʽ���̣��ʱ�ѡ����ȷ��
��ѡD�� ���������εĶԳ�����______��
 ����ƽ��������ֱ��
��������һ��ͼ����һ��ֱ�߶��ۣ�ֱ�����ԵIJ����ܹ���ȫ�غϣ���ô���ͼ�ξ�����Գ�ͼ�Σ�����ֱ�߾������ͼ�ε�һ���Գ���,��ͼ��ʾ�����������εĶԳ����Ƕ���ƽ��������ֱ��.
�ʴ��ǣ�����ƽ��������ֱ��.
����ƽ��������ֱ��
��������һ��ͼ����һ��ֱ�߶��ۣ�ֱ�����ԵIJ����ܹ���ȫ�غϣ���ô���ͼ�ξ�����Գ�ͼ�Σ�����ֱ�߾������ͼ�ε�һ���Գ���,��ͼ��ʾ�����������εĶԳ����Ƕ���ƽ��������ֱ��.
�ʴ��ǣ�����ƽ��������ֱ��. 
