如图，在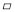
ABCD中，点E在CD边上运动(不与C，D两点重合)，连结AE并延长与BC的延长线交于点F.连结BE，DF，若△BCE的面积为8，则△DEF的面积为________．
8
【解析】试题解析：
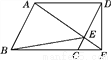
故答案为： 如图，在平行四边形ABCD中，若AB=6，AD=10，∠ABC的平分线交AD于点E，交CD的延长线于点F，求DF的长．
4
【解析】
试题分析：首先根据平行四边形的性质可得AB=DC=6，AD=BC=10，AB∥DC，再根据平行线的性质与角平分线的性质证明∠2=∠3，根据等角对等边可得BC=CF=10，再用CF﹣CD即可算出DF的长．
试题解析：∵四边形ABCD为平行四边形，∴AB=DC=6，AD=BC=10，AB∥DC． ∵AB∥DC，∴∠1=∠3，
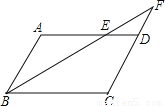
又∵BF平分∠ABC，∴∠1=∠2，∴... 在平行四边形ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，可得答案；
（2）根据平行线的性质，可得∠DFA=∠FAB，根据等腰三角形的判定与性质，可得∠DAF=∠DFA，根据角平分线的判定，可得答案．
试题分析：（1）证明：∵四边形ABCD是平行四边形，
∴AB∥C... 如图，在□ABCD中，AC交BD于点O，点E、点F分别是OA、OC的中点，请判断线段BE、DF的关系，并证明你的结论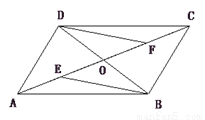
【解析】根据平行四边形的性质对角线互相平分得出OA=OC，OB=OD，利用中点的意义得出OE=OF，从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形，从而得出BE=DF，BE∥DF．
【解析】
由题意得：BE=DF，BE∥DF．理由如下：
连接DE、BF．
∵ABCD是平行四边形，
∴OA=OC，OB=OD，
∵E，F分别是... ( 本小题满分10分)如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：
⑴△AEH≌△CGF；
⑵四边形EFGH是菱形．
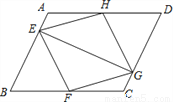
（1）证明见试题解析；（2）证明见试题解析．
【解析】试题分析：(1)、由全等三角形的判定定理SAS证得结论；(2)、易证四边形EFGH是平行四边形，那么EF∥GH，那么∠HGE=∠FEG，而EG是角平分线，易得∠HEG=∠FEG，根据等量代换可得∠HEG=∠HGE，从而有HE=HG，易证四边形EFGH是菱形．
试题解析：（1）、如图，∵四边形ABCD是平行四边形， ∴∠A=∠C，
... 如图，□ABCD中，E是BC边的中点，连接AE，F为CD边上一点，且满足∠DFA=2∠BAE．
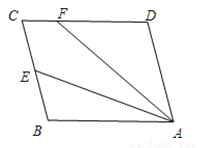
（1）若∠D=105°，∠DAF=35°．求∠FAE的度数；
（2）求证：AF=CD+CF．
（1）20°；（2）见解析
【解析】试题分析：（1）根据平行四边形的性质、平行线的性质证得；然后结合已知条件求得从而求得的度数；
（2）在AF上截取连接利用全等三角形的判定定理SAS证得 ≌，由全等三角形的对应角相等、对应边相等；然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得 最后根据线段间的和差关系证得结论．
试题解析：
（三角形内角和定理）．
∵四边... 如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（ ）
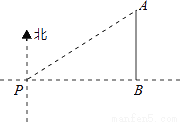
A. 2海里 B. 2sin55°海里 C. 2cos55°海里 D. 2tan55°海里
C
【解析】试题分析：首先由方向角的定义及已知条件得出∠NPA=55°，AP=2海里，∠ABP=90°，再由AB∥NP，根据平行线的性质得出∠A=∠NPA=55°．然后解Rt△ABP，得出AB=AP•cos∠A=2cos55°海里．
【解析】
如图，由题意可知∠NPA=55°，AP=2海里，∠ABP=90°．
∵AB∥NP，
∴∠A=∠NPA=55°．
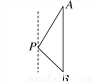
在Rt△AB... 如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔60海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为( )
A. 30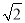
海里 B. 30
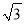海里 C. 60海里 D. 30
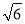海里
A
【解析】试题分析：过点P作PC⊥AB于点C． 在Rt△PAC中，∵PA=60海里，∠PAC=30°， ∴CP=AP=30海里．
在Rt△PBC中，∵PC=30海里，∠PBC=∠BPC=45°， ∴PB=PC=30海里．
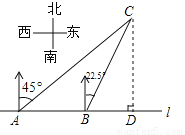
即海轮所在的B处与灯塔P的距离为30海里． 如图，在一笔直的海岸线l上有A、B两个观测站，AB=2km、从A测得船C在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则船C离海岸线l的距离（即CD的长）为（ ）
A. 4km B. （2+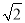
）km C. 2
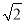km D. （4-
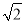）km
B
【解析】试题分析：根据题意中方位角的特点，过点B作BE⊥AC，交AC于点E，由∠CAB=45°，AB=2km，可知BE=km，根据题意还可知∠BCA=∠BCD=22.5°，因此CB是∠ACD的角平分线，根据角平分线的性质可得：BD=BE=km，因此CD=AD=AB+BD=(2+)km，故选B． 如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为（ ）
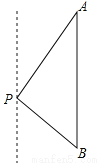
A. 40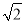
海里 B. 40
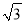海里 C. 80海里 D. 40
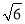海里
A
【解析】试题分析：过点P作PD⊥AB于点D，根据方位角可得：∠A=30°，∠B=45°，根据AP=80海里可得PD=40海里，PB=40海里，故选A．