��Ŀ����
��ͼ����ABCD�У�E��BC�ߵ��е㣬����AE��FΪCD����һ�㣬�������DFA=2��BAE��
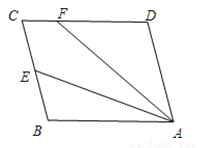
��1������D=105�㣬��DAF=35�㣮���FAE�Ķ�����
��2����֤��AF=CD+CF��
 ��1��20�㣻��2��������
�������������������1������ƽ���ı��ε����ʡ�ƽ���ߵ�����֤�ã�Ȼ������֪������ôӶ���õĶ�����
��2����AF�Ͻ�ȡ��������ȫ�������ε��ж�����SAS֤�� �գ���ȫ�������εĶ�Ӧ����ȡ���Ӧ����ȣ�Ȼ�����е�E������ƽ���ߵ������Լ����������ε��ж���������� �������߶μ�ĺͲ��ϵ֤�ý��ۣ�
���������
���������ڽǺͶ�������
���ı�...
��1��20�㣻��2��������
�������������������1������ƽ���ı��ε����ʡ�ƽ���ߵ�����֤�ã�Ȼ������֪������ôӶ���õĶ�����
��2����AF�Ͻ�ȡ��������ȫ�������ε��ж�����SAS֤�� �գ���ȫ�������εĶ�Ӧ����ȡ���Ӧ����ȣ�Ȼ�����е�E������ƽ���ߵ������Լ����������ε��ж���������� �������߶μ�ĺͲ��ϵ֤�ý��ۣ�
���������
���������ڽǺͶ�������
���ı�...
 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д������κ���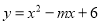 �䷽��Ϊ
�䷽��Ϊ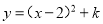 ����m��k��ֵ�ֱ�Ϊ�� ��
����m��k��ֵ�ֱ�Ϊ�� ��
A. 0��6
B. 0��2
C. 4��6
D. 4��2
 D
���������ߣ�
��
�࣬
��-4=-m��4+k=6��
��m=4��k=2��
��ѡ��D��
D
���������ߣ�
��
�࣬
��-4=-m��4+k=6��
��m=4��k=2��
��ѡ��D�� ����2��x��1ʱ�����κ���y=����x��m��2+m2+1�����ֵ4����ʵ��m��ֵΪ��������
A. ��2 B. 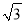 ��-
��-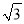 C. 2��-
C. 2��-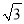 D. 2��
D. 2��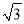 ��-
��-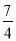
 C
��������������ø������ߵĶԳ���Ϊx=m.
�ٵ�-2��m��1ʱ,��ʱ���ֵΪ,��=4,
���m= (��ȥ)��m=-;
�ڵ�m>1ʱ,��ʱ��x=1ʱ,���������ֵ,����,
���m=2;
�۵�m<-2ʱ,��ʱx=-2���������ֵ,����,
���m= (��������,��ȥ).
��������,m= -��m=2.
����Cѡ������ȷ��.
C
��������������ø������ߵĶԳ���Ϊx=m.
�ٵ�-2��m��1ʱ,��ʱ���ֵΪ,��=4,
���m= (��ȥ)��m=-;
�ڵ�m>1ʱ,��ʱ��x=1ʱ,���������ֵ,����,
���m=2;
�۵�m<-2ʱ,��ʱx=-2���������ֵ,����,
���m= (��������,��ȥ).
��������,m= -��m=2.
����Cѡ������ȷ��. ������һ��С��A��������Χa�������а������洬������Ⱥ�������У���B����С��A�ڱ�ƫ��75�㷽���ϣ�����12���ﵽ��D�㣬���Dz��С��A�ڱ�ƫ��60�㷽���ϣ����洬���ı亽�������ж�û�д���Σ�գ���a�����ֵΪ��������
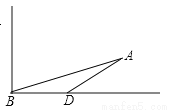
A. 5 B. 6 C. 6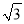 D. 8
D. 8
 B
�������������������AC��BD�ڵ�C�� ��ABD=90��-75��=15�㣬
�ߡ�ADC=90��-60��=30�㣬 ���BAD=��ADC-��ABD=30��-15��=15�㣬
���ABD=��BAD�� ��BD=AD=12�������
��ֱ�ǡ�ADC�У�AC=AD=��12=6���������ѡB��
B
�������������������AC��BD�ڵ�C�� ��ABD=90��-75��=15�㣬
�ߡ�ADC=90��-60��=30�㣬 ���BAD=��ADC-��ABD=30��-15��=15�㣬
���ABD=��BAD�� ��BD=AD=12�������
��ֱ�ǡ�ADC�У�AC=AD=��12=6���������ѡB�� ��ͼ���ۿ�A�ڹ۲�վO����������OA=4km��ij���Ӹۿ�A�������ر�ƫ��15�㷽����һ�ξ����B������ʱ�ӹ۲�վO����øô�λ�ڱ�ƫ��60��ķ�����ô����еľ��루��AB�ij���Ϊ��������
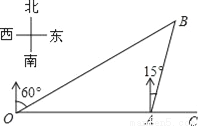
A. 4km B. 2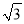 km C. 2
km C. 2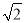 km D. ��
km D. ��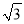 +1��km
+1��km
 C
���������������������A��AD��OB����AD=OA=2km����������ɵã���ABDΪ����ֱ�������Σ���AB=2km.
C
���������������������A��AD��OB����AD=OA=2km����������ɵã���ABDΪ����ֱ�������Σ���AB=2km. ��ͼ����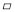 ABCD�У���E��CD�����˶�(����C��D�����غ�)������AE���ӳ���BC���ӳ��߽��ڵ�F.����BE��DF������BCE�����Ϊ8�����DEF�����Ϊ________��
ABCD�У���E��CD�����˶�(����C��D�����غ�)������AE���ӳ���BC���ӳ��߽��ڵ�F.����BE��DF������BCE�����Ϊ8�����DEF�����Ϊ________��
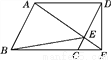
 8
�����������������
�ʴ�Ϊ��
8
�����������������
�ʴ�Ϊ�� ��ͼ��������ABCD��AE��BC���ϵĸߣ���֪AE=4��CE=8��������ABCD������ǣ�������
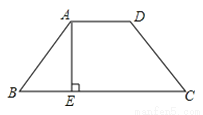
A. 16 B. 32 C. 24 D. 48
 B
���������������������C��CF��AD��AD���ӳ����ڵ�F�����CFD=90�㣮
���ı���ABCD�ǵ�������
��AD��BC��AB=CD��
�֡�AE��BC���ϵĸߣ�
���ı���AECF�Ǿ��Σ�
�ں���
�գ�HL����
������ABCD�����=����AECF�����=4��8=32��
��ѡB��
B
���������������������C��CF��AD��AD���ӳ����ڵ�F�����CFD=90�㣮
���ı���ABCD�ǵ�������
��AD��BC��AB=CD��
�֡�AE��BC���ϵĸߣ�
���ı���AECF�Ǿ��Σ�
�ں���
�գ�HL����
������ABCD�����=����AECF�����=4��8=32��
��ѡB�� ���һ������ε��ڽǺ���������Ǻ���ȣ���ô����������____����
 ��
���������߶���ε���Ǻ�Ϊ360�㣬
��һ������ε��ڽǺ���������Ǻ�������ȣ�����������Ϊn���Σ�
�ࣨn-2��•180��=360�㣬
��n=4��
�ʴ�Ϊ���ģ�
��
���������߶���ε���Ǻ�Ϊ360�㣬
��һ������ε��ڽǺ���������Ǻ�������ȣ�����������Ϊn���Σ�
�ࣨn-2��•180��=360�㣬
��n=4��
�ʴ�Ϊ���ģ� ��x=( )ʱ, 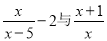 ��Ϊ�෴��.
��Ϊ�෴��.
A. 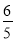 B.
B. 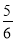 C.
C. 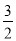 D.
D. 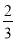
 B
��������������ã� .��ѡB.
B
��������������ã� .��ѡB. 
