题目内容
如图,在□ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断线段BE、DF的关系,并证明你的结论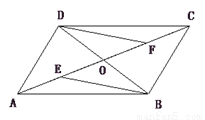
 【解析】根据平行四边形的性质对角线互相平分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形,从而得出BE=DF,BE∥DF.
【解析】
由题意得:BE=DF,BE∥DF.理由如下:
连接DE、BF.
∵ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是...
【解析】根据平行四边形的性质对角线互相平分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形,从而得出BE=DF,BE∥DF.
【解析】
由题意得:BE=DF,BE∥DF.理由如下:
连接DE、BF.
∵ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是...
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
若二次函数y=ax2+bx+c的x与y的部分对应值如下表,则当x=1时,y的值为( )
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
A. -27
B. -13
C. -3
D. 5
 A
【解析】设二次函数的解析式为,
∵当x=-4或-2时,y=3,由抛物线的对称性可知h=-3,k=5,
∴,
把(-2,3)代入得,a=-2,
∴二次函数的解析式为,
当x=1时,y=-27.
故选:A.
A
【解析】设二次函数的解析式为,
∵当x=-4或-2时,y=3,由抛物线的对称性可知h=-3,k=5,
∴,
把(-2,3)代入得,a=-2,
∴二次函数的解析式为,
当x=1时,y=-27.
故选:A. 如果点(-2,-3)和(5,-3)都是抛物线y=ax2+bx+c上的点,那么抛物线的对称轴是 ( )
A. x=3 B. x=-3 C. x=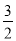 D. x=-
D. x=-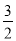
 C
【解析】点(?2,?3)和(5,?3)都是抛物线y=ax²+bx+c上的点,得
(?2,?3)、(5,?3)关于对称轴对称,
即对称轴过(?2,?3)、(5,?3)的中点,
x=,
故选C.
C
【解析】点(?2,?3)和(5,?3)都是抛物线y=ax²+bx+c上的点,得
(?2,?3)、(5,?3)关于对称轴对称,
即对称轴过(?2,?3)、(5,?3)的中点,
x=,
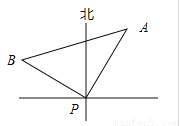
故选C. 某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行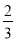 小时到达B处,那么tan∠BAP=( )
小时到达B处,那么tan∠BAP=( )
A. 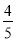 B.
B. 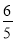 C.
C. 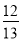 D.
D. 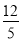
 A
【解析】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A.
A
【解析】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
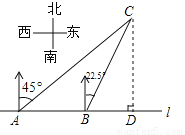
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A. 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A. 4km B. (2+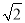 )km C. 2
)km C. 2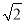 km D. (4-
km D. (4-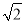 )km
)km
 B
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B.
B
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B. 在□ABCD中,对角线AC,BD相交于点O,AB=8cm,BC=6cm.△AOB的周长是18cm,则△AOD的周长是__________.
 16cm
【解析】试题解析:
如图所示:
∵四边形ABCD是平行四边形,
的周长是18cm,AB=8cm,
的周长
故答案为:16cm.
16cm
【解析】试题解析:
如图所示:
∵四边形ABCD是平行四边形,
的周长是18cm,AB=8cm,
的周长
故答案为:16cm. 如图,等腰梯形ABCD下底与上底的差恰好等于腰长,DE∥AB.则∠DEC等于( )
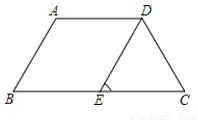
A. 75° B. 60° C. 45° D. 30°
 B
【解析】试题解析:∵DE∥AB,AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵BC-AD=AB=EC,
∵等腰梯形ABCD,
∴AB=DC=EC,
∴为等边三角形,
∴∠DEC=60°.
故选B.
B
【解析】试题解析:∵DE∥AB,AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵BC-AD=AB=EC,
∵等腰梯形ABCD,
∴AB=DC=EC,
∴为等边三角形,
∴∠DEC=60°.
故选B. 一个多边形的每个外角都是36°,这个多边形是______边形
 十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十.
十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十. 下列关于x的方程是分式方程的是( )
A. 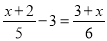 ; B.
; B. 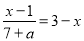 ; C.
; C. 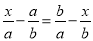 ; D.
; D. 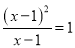
 D
【解析】根据分式方程的定义——分母中含有未知数的方程.故选D.
D
【解析】根据分式方程的定义——分母中含有未知数的方程.故选D. 
