题目内容
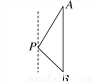
如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔60海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为( )
A. 30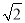
海里 B. 30
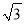海里 C. 60海里 D. 30
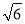海里
A
【解析】试题分析：过点P作PC⊥AB于点C． 在Rt△PAC中，∵PA=60海里，∠PAC=30°， ∴CP=AP=30海里．
在Rt△PBC中，∵PC=30海里，∠PBC=∠BPC=45°， ∴PB=PC=30海里．
即海轮所在的B处与灯塔P的距离为30海里．
金钥匙试卷系列答案一个二次函数的图象经过点A（0，0），B（-1，-11），C（1，9）三点，则这个二次函数的关系式是（ ）
A.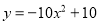 
B.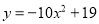 
C.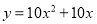 
D.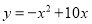 
D
【解析】由于抛物线经过原点，则可以设其函数关系式为，
将B、C两点坐标代入，得
解得
则函数关系式为
故选：D． 将抛物线y=x2向左平移4个单位后，再向下平移2个单位，则此时抛物线的解析式是________．
y=（x+4）2-2
【解析】∵y=x2向左平移4个单位后,再向下平移2个单位. ∴y= .故此时抛物线的解析式是y=.故答案为：y=（x+4）2-2. 温州市处于东南沿海，夏季经常遭受台风袭击．一次，温州气象局测得台风中心在温州市A的正西方向300千米的B处（如图），以每小时10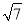
千米的速度向东偏南30°的BC方向移动，并检测到台风中心在移动过程中，温州市A将受到影响，且距台风中心200千米的范围是受台风严重影响的区域．则影响温州市A的时间会持续多长？（ ）
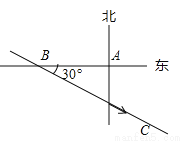
A. 5 B. 6 C. 8 D. 10
D
【解析】试题分析：过点A作AD⊥BC于D，由题意得AB=300，∠ABD＝30°，∴AD =150（km），
温州市点A受到台风严重影响设风台中心距A点200km处，刚好处在BC上的E，F两点
则在Rt△ADE中，AE＝200，AD＝150 ∴DE=50km， ∴EF=2DE=100km，
则t=100÷10=10h，故选D． 如图，C、D分别是一个湖的南、北两端A和B正东方向的两个村庄，CD=6km，且D位于C的北偏东30°方向上，则AB的长为（ ）
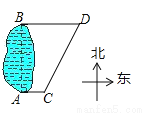
A. 2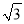
km B. 3
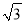km C.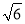 
km D. 3km
B
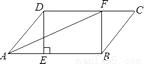
【解析】试题分析：过点C作CE⊥BD，则∠DCE=30°，根据CD=6km可得：CE=3km，故AB=CE=3km，故选B． 在平行四边形ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，可得答案；
（2）根据平行线的性质，可得∠DFA=∠FAB，根据等腰三角形的判定与性质，可得∠DAF=∠DFA，根据角平分线的判定，可得答案．
试题分析：（1）证明：∵四边形ABCD是平行四边形，
∴AB∥C... 如图，□ABCD的周长为16 cm，AC，BD相交于点O，EO⊥BD交AD于点E，则△ABE的周长为( )
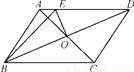
A. 4 cm B. 6 cm C. 8 cm D. 10 cm
C
【解析】试题解析：∵四边形ABCD是平行四边形，
∴AB=DC，AD=BC，BO=DO，
∵EO⊥BO，
∴BE=DE，
故选C. n边形的外角和与内角和的度数之比为2:7,则边数为______
9
【解析】由题意得：
（n-2）•180°：360°=7：2，
解得n=9，
故答案为：9． 某工地调来72人挖土和运土,已知3人挖出的土1人恰好能全部运走,怎样调配劳动力使挖出的土能及时运走且窝工,解决此问题可设派x人挖土,其它人运土,列方程:
①x+3x=72, ②72-x=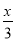
, ③
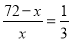, ④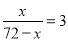
.
上述所列方程正确的( )
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】设派x人挖土,则（72-x）人运土，根据3人挖出的土1人恰好能全部运走列方程：运土的人数是挖土人数的 ，即 或 或；故②、 ③ ④正确；故选C..