题目内容
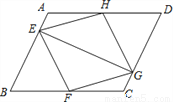
( 本小题满分10分)如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：
⑴△AEH≌△CGF；
⑵四边形EFGH是菱形．
（1）证明见试题解析；（2）证明见试题解析．
【解析】试题分析：(1)、由全等三角形的判定定理SAS证得结论；(2)、易证四边形EFGH是平行四边形，那么EF∥GH，那么∠HGE=∠FEG，而EG是角平分线，易得∠HEG=∠FEG，根据等量代换可得∠HEG=∠HGE，从而有HE=HG，易证四边形EFGH是菱形．
试题解析：（1）、如图，∵四边形ABCD是平行四边形， ∴∠A=∠C，
...
练习册系列答案
阅读快车系列答案
相关题目
将二次函数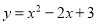
化为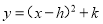
的形式，结果为（ ）
A.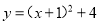 
B.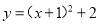 
C.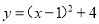 
D.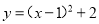 
D
【解析】
故选：D． 二次函数y=ax2+bx+c满足b2=ac，且x=0时，y=﹣4，则（ ）
A. y最大=﹣4 B. y最小=﹣4 C. y最大=﹣3 D. y最小=﹣3
C
【解析】试题分析：将x=0，y=-4代入可得：c=-4，根据可得： ，故函数有最大值，则最大值为： ，故选C． 如图，在一次夏令营活动中，小霞同学从营地A点出发，要到距离A点10千米的C地去，先沿北偏东70°方向走了8千米到达B地，然后再从B地走了6千米到达目的地C，此时小霞在B地的（ ）
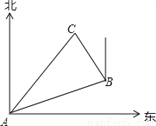
A. 北偏东20°方向上 B. 北偏西20°方向上
C. 北偏西30°方向上 D. 北偏西40°方向上
B
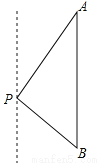
【解析】试题分析：根据题意可得：∠DAB=70°，AD∥BE，AC=10，AB=8，BC=6，根据勾股定理的逆定理可知∠ABC=90°，根据平行线的性质可得：∠ABE=110°，则∠CBE=110°-90°=20°，即点C在点B的北偏西20°方向上. 如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为（ ）
A. 40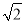
海里 B. 40
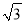海里 C. 80海里 D. 40
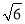海里
A
【解析】试题分析：过点P作PD⊥AB于点D，根据方位角可得：∠A=30°，∠B=45°，根据AP=80海里可得PD=40海里，PB=40海里，故选A． 一个平行四边形两对角之和为116°，则相邻的两内角分别是__________和_________．
58° 122°
【解析】试题解析：
如图所示：
∵四边形ABCD是平行四边形，
故答案为：58°；122°． 如图，在□ABCD中，点M为CD的中点，且DC=2AD，则AM与BM的夹角的度数为（ ）
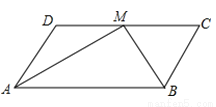
A. 100° B. 95° C. 90° D. 85°
C
【解析】试题解析： 中，
∴DC∥AB，AD∥BC，
∴∠DAB+∠CBA=180°，∠BAM=∠DMA，
∵点M为CD的中点，且DC=2AD，
∴DM=AD，
∴∠DMA=∠DAM，
∴∠DAM=∠BAM，
同理∠ABM=∠CBM，
即：
∴∠AMB=180°-90°=90°．
故选C． 若n边形的每个内角都等于150°，则n=_____．
12
【解析】试题解析：由题意可得：
解得
故多边形是12边形．
故答案为：12． 下列关于分式方程增根的说法正确的是（ ）
A．使所有的分母的值都为零的解是增根
B．分式方程的解为零就是增根
C．使分子的值为零的解就是增根
D．使最简公分母的值为零的解是增根
D
【解析】
试题分析：分式方程的增根是最简公分母为零时，未知数的值．
【解析】
分式方程的增根是使最简公分母的值为零的解．
故选D．