题目内容
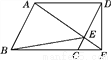
如图,在 ABCD中,点E在CD边上运动(不与C,D两点重合),连结AE并延长与BC的延长线交于点F.连结BE,DF,若△BCE的面积为8,则△DEF的面积为________.
ABCD中,点E在CD边上运动(不与C,D两点重合),连结AE并延长与BC的延长线交于点F.连结BE,DF,若△BCE的面积为8,则△DEF的面积为________.
 8
【解析】试题解析:
故答案为:
8
【解析】试题解析:
故答案为:
练习册系列答案
相关题目
如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于( )
A. 8
B. 14
C. 8或14
D. -8或-14
 C
【解析】根据题意,得
,
解得c=8或14.
故选:C.
C
【解析】根据题意,得
,
解得c=8或14.
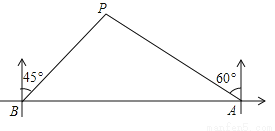
故选:C. 如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
 小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里
【解析】试题分析:过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、AM、BP.
试题解析:如图:过P作PM⊥AB于M,则∠PMB=∠PMA=90°,∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20,∴PM=AP=10,AM=PM=,∴∠BPM=...
小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里
【解析】试题分析:过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、AM、BP.
试题解析:如图:过P作PM⊥AB于M,则∠PMB=∠PMA=90°,∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20,∴PM=AP=10,AM=PM=,∴∠BPM=... 如图,C、D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为( )
A. 2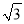 km B. 3
km B. 3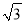 km C.
km C. 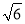 km D. 3km
km D. 3km
 B
【解析】试题分析:过点C作CE⊥BD,则∠DCE=30°,根据CD=6km可得:CE=3km,故AB=CE=3km,故选B.
B
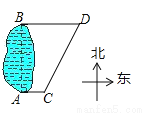
【解析】试题分析:过点C作CE⊥BD,则∠DCE=30°,根据CD=6km可得:CE=3km,故AB=CE=3km,故选B. 如图,□ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.
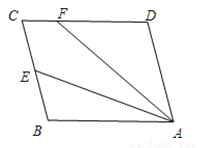
(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;
(2)求证:AF=CD+CF.
 (1)20°;(2)见解析
【解析】试题分析:(1)根据平行四边形的性质、平行线的性质证得;然后结合已知条件求得从而求得的度数;
(2)在AF上截取连接利用全等三角形的判定定理SAS证得 ≌,由全等三角形的对应角相等、对应边相等;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得 最后根据线段间的和差关系证得结论.
试题解析:
(三角形内角和定理).
∵四边...
(1)20°;(2)见解析
【解析】试题分析:(1)根据平行四边形的性质、平行线的性质证得;然后结合已知条件求得从而求得的度数;
(2)在AF上截取连接利用全等三角形的判定定理SAS证得 ≌,由全等三角形的对应角相等、对应边相等;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得 最后根据线段间的和差关系证得结论.
试题解析:
(三角形内角和定理).
∵四边... 如图,□ABCD的周长为16 cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
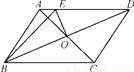
A. 4 cm B. 6 cm C. 8 cm D. 10 cm
 C
【解析】试题解析:∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC,BO=DO,
∵EO⊥BO,
∴BE=DE,
故选C.
C
【解析】试题解析:∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC,BO=DO,
∵EO⊥BO,
∴BE=DE,
故选C. 如图,?ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( )
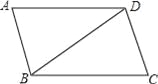
A. 16° B. 22° C. 32° D. 68°
 C
【解析】试题分析:根据平行四边形的性质可知:AD∥BC,所以∠C+∠ADC=180°,再由BC=BD可得∠C=∠BDC=74°,进而可求出∠ADB=106°﹣74°=32°.
故选:C.
C
【解析】试题分析:根据平行四边形的性质可知:AD∥BC,所以∠C+∠ADC=180°,再由BC=BD可得∠C=∠BDC=74°,进而可求出∠ADB=106°﹣74°=32°.
故选:C. 内角和等于外角和2倍的多边形是( )
A. 五边形 B. 六边形 C. 七边形 D. 八边形
 B
【解析】试题分析:本题应先设这个多边形的边数为n,则依题意可列出方程(n﹣2)×180°=360°×2,从而解出n=6,即这个多边形的边数为6.
【解析】
设这个多边形的边数为n,则依题意可得:
(n﹣2)×180°=360°×2,
解得n=6,
∴这个多边形的边数为6.
故选B.
B
【解析】试题分析:本题应先设这个多边形的边数为n,则依题意可列出方程(n﹣2)×180°=360°×2,从而解出n=6,即这个多边形的边数为6.
【解析】
设这个多边形的边数为n,则依题意可得:
(n﹣2)×180°=360°×2,
解得n=6,
∴这个多边形的边数为6.
故选B. 下列各式从左到右的变形正确的是( )
A.  B.
B. 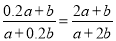
C. 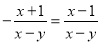 D.
D. 
 A
【解析】选项A:分子分母同时乘以2得到答案,正确;
选项B: ==,所以错误;
选项C: ==,所以错误;
选项D: ==,所以错误.
故选:A.
A
【解析】选项A:分子分母同时乘以2得到答案,正确;
选项B: ==,所以错误;
选项C: ==,所以错误;
选项D: ==,所以错误.
故选:A. 
