已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(1,4)和点(5,0),则该抛物线的解析式为__________.
 y=-0.5x+2x-2.5
【解析】∵抛物线对称轴是直线x=2且经过点A(5,0),
由抛物线的对称性可知:抛物线还经过点(?1,0),
设抛物线的解析式为y=a(x?x1)(x?x2)(a≠0),
即:y=a(x+1)(x?5),
把(1,4)代入得:4=?8a,
∴a=?.
∴抛物线的解析式为:y=?x2+2x+.
故答案为:y=?x2+2x+...
y=-0.5x+2x-2.5
【解析】∵抛物线对称轴是直线x=2且经过点A(5,0),
由抛物线的对称性可知:抛物线还经过点(?1,0),
设抛物线的解析式为y=a(x?x1)(x?x2)(a≠0),
即:y=a(x+1)(x?5),
把(1,4)代入得:4=?8a,
∴a=?.
∴抛物线的解析式为:y=?x2+2x+.
故答案为:y=?x2+2x+... 用配方法把二次函数y=l+2x-x2化为y=a(x-h)2+k的形式,作出它的草图,回答下列问题.
(1)求抛物线的顶点坐标和它与x轴的交点坐标;
(2)当x取何值时,y随x的增大而增大?
(3)当x取何值时,y的值大于0?
 y=-(x-1)2+2(1)顶点坐标为(1,2),与x轴的两个交点坐标分别为(1-,0),(1+,0)(2)当x<1时,y随x的增大而增大.(3)当l-<x<1+时,y的值大于0
【解析】分析:(1)利用配方法得到y=-(x-1)²+2,则根据二次函数的性质可得到抛物线的顶点坐标;再利用抛物线与x轴的交点问题,通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标;(2)根据二次函数的性质...
y=-(x-1)2+2(1)顶点坐标为(1,2),与x轴的两个交点坐标分别为(1-,0),(1+,0)(2)当x<1时,y随x的增大而增大.(3)当l-<x<1+时,y的值大于0
【解析】分析:(1)利用配方法得到y=-(x-1)²+2,则根据二次函数的性质可得到抛物线的顶点坐标;再利用抛物线与x轴的交点问题,通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标;(2)根据二次函数的性质... 把8米长的钢筋,焊成一个如图所示的框架,使其下部为矩形,上部为半圆形.请你写出钢筋所焊成框架的面积y(平方米)与半圆的半径x(米)之间的函数关系式.

 y=-(π+2)x2+8x
【解析】分析:如图可求出半圆的面积以及一个长方形面积,然后可求出y与x之间的函数关系式.
本题解析:
半圆面积: πx2.
长方形面积: ×2x(8-2x-πx)=8x-(2+π)x2.
∴y=πx2+8x-(2+π)x2,
即y=-(π+2)x2+8x,
y=-(π+2)x2+8x
【解析】分析:如图可求出半圆的面积以及一个长方形面积,然后可求出y与x之间的函数关系式.
本题解析:
半圆面积: πx2.
长方形面积: ×2x(8-2x-πx)=8x-(2+π)x2.
∴y=πx2+8x-(2+π)x2,
即y=-(π+2)x2+8x, 已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
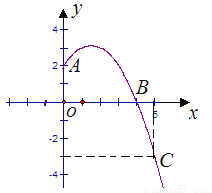
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
 (1)抛物线y =顶点(,)(2)略(3) 当-1<x<4时, y >0
【解析】试题分析:本题的关键是求出抛物线的解析式,在题目给出的图象中可得出A、B、C三点的坐标,可用待定系数求出抛物线的解析式,进而可画出x<0时抛物线的图象,以及y>0时x的取值范围.
【解析】
(1)由图象,可知A(0,2),B(4,0),C(5,﹣3),
得方程组.
解得a=﹣,b=,c=2....
(1)抛物线y =顶点(,)(2)略(3) 当-1<x<4时, y >0
【解析】试题分析:本题的关键是求出抛物线的解析式,在题目给出的图象中可得出A、B、C三点的坐标,可用待定系数求出抛物线的解析式,进而可画出x<0时抛物线的图象,以及y>0时x的取值范围.
【解析】
(1)由图象,可知A(0,2),B(4,0),C(5,﹣3),
得方程组.
解得a=﹣,b=,c=2.... 已知抛物线y=ax2+bx+c的大致图象如图所示,试确定a,b,c,b2-4ac及a+b+c的符号.
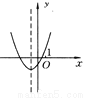
 a+b+c>0
【解析】分析:根据二次函数的图形确定a、b、c的符号,根据抛物线与x轴的交点确定的符号,由当x=1时,函数值的符号确定a+b+c的符号.
本题解析:
∵抛物线开口向上,∴a>0.∵抛物线与y轴的交点在y轴的负半轴上,∴C<0.又∵对称轴在y轴左侧,∴ab>0.∵a>0,∴b>0.∵抛物线与x轴有两个交点,∴△=b2-4ac>0.∵当x=1时,y>0,∴a+b+c>...
a+b+c>0
【解析】分析:根据二次函数的图形确定a、b、c的符号,根据抛物线与x轴的交点确定的符号,由当x=1时,函数值的符号确定a+b+c的符号.
本题解析:
∵抛物线开口向上,∴a>0.∵抛物线与y轴的交点在y轴的负半轴上,∴C<0.又∵对称轴在y轴左侧,∴ab>0.∵a>0,∴b>0.∵抛物线与x轴有两个交点,∴△=b2-4ac>0.∵当x=1时,y>0,∴a+b+c>... ―抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
 (1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析...
(1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析... 如图所示,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的.点O′在x轴的正半轴上,点B的坐标为(1,3).
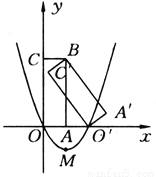
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点,且图象顶点M的纵坐标为-l,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
(3)求边C′O′所在直线的解析式.
 (1) y=x2-2x(2)1(3)y=
【解析】分析:(1)连接BO,B则B0=B,求出M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知 (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析:(1)如图2-83所示,连...
(1) y=x2-2x(2)1(3)y=
【解析】分析:(1)连接BO,B则B0=B,求出M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知 (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析:(1)如图2-83所示,连... 分式方程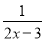 =l的解为 ( )
=l的解为 ( )
A. x=2 B. x=l C. x=-l D. x=-2
 A
【解析】方程两边同乘(2x-3),得
1=2x-3,
解得:x=2,
经检验,x=2是原方程的解,
故选A.
A
【解析】方程两边同乘(2x-3),得
1=2x-3,
解得:x=2,
经检验,x=2是原方程的解,
故选A. 某煤矿原计划x天生存120t煤,由于采用新的技术,每天增加生存3t,因此提前2天完成,列出的方程为( )
A. 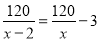 B.
B. 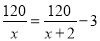
C. 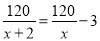 D.
D. 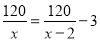
 D
【解析】因为原计划x天生产120吨煤,所以原计划每天生产吨,因为采取新的技术,提前2天 ,所以现在每天生产吨,因为现在每天比原计划每天增加3吨,所以可列方程是,故选D.
D
【解析】因为原计划x天生产120吨煤,所以原计划每天生产吨,因为采取新的技术,提前2天 ,所以现在每天生产吨,因为现在每天比原计划每天增加3吨,所以可列方程是,故选D. 若分式方程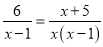 有增根,则增根是( )
有增根,则增根是( )
A. x=1 B. x=1或x=0 C. x=0 D. 不确定
 A
【解析】方程两边同乘x(x-1),得
6x=x+5,
解得:x=1,
检验:当x=1时,x(x-1)=0,所以x=1是原方程的增根,原方程无解,
故选A.
A
【解析】方程两边同乘x(x-1),得
6x=x+5,
解得:x=1,
检验:当x=1时,x(x-1)=0,所以x=1是原方程的增根,原方程无解,
故选A.