题目内容
如图所示，矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上，边OC在y轴正半轴上)绕点B逆时针旋转得到的．点O′在x轴的正半轴上，点B的坐标为(1，3)．
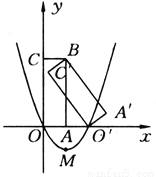
(1)如果二次函数y＝ax2+bx+c（a≠0)的图象经过O，O′两点，且图象顶点M的纵坐标为－l，求这个二次函数的解析式；
(2)在(1)中求出的二次函数图象对称轴的右侧，是否存在点P，使得△POM为直角三角形?若存在，求出点P的坐标和△POM的面积；若不存在，请说明理由；
(3)求边C′O′所在直线的解析式．
(1) y＝x2－2x(2)1(3)y=
【解析】分析:(1)连接BO,B则B0=B,求出M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知 (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析：(1)如图2－83所示，连...
考前必练系列答案若点A（2， 
），B（-3，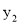 
），C（-1， 
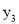）三点在抛物线
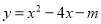的图象上，则
、
、
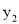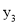的大小关系是（ ）
A.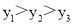 
B.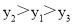 
C.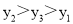 
D.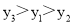 
C
【解析】首先求出二次函数的图象的对称轴x==2，且由a=1＞0，可知其开口向上，然后由A（2， ）中x=2，知最小，再由B（-3， ），C（-1， ）都在对称轴的左侧，而在对称轴的左侧，y随x得增大而减小，所以．总结可得．
故选：C． 若二次函数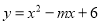
配方后为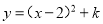
，则m，k的值分别为（ ）
A. 0，6
B. 0，2
C. 4，6
D. 4，2
D
【解析】∵，
，
∴，
∴-4=-m，4+k=6，
∴m=4，k=2．
故选：D． 若分式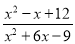
的值为１，则x＝____．
3
【解析】由题意得=１，
解得：x=3，
经检验x=3是分式方程的解，
故答案为：3. 解分式方程的基本思想是把分式方程化为_________，最后要注意_________．
整式方程 检验
【解析】解分式方程的基本思想是把分式方程化为整式方程，最后要注意检验，
故答案为：整式方程，检验． 用配方法把二次函数y＝l+2x－x2化为y＝a(x－h)2+k的形式，作出它的草图，回答下列问题．
(1)求抛物线的顶点坐标和它与x轴的交点坐标；
(2)当x取何值时，y随x的增大而增大?
(3)当x取何值时，y的值大于0?
y=－(x－1)2＋2(1)顶点坐标为(1，2)，与x轴的两个交点坐标分别为(1－，0)，(1＋，0)(2)当x＜1时，y随x的增大而增大.(3)当l－＜x＜1＋时，y的值大于0
【解析】分析：（1）利用配方法得到y=-(x-1)²+2，则根据二次函数的性质可得到抛物线的顶点坐标；再利用抛物线与x轴的交点问题，通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标；（2）根据二次函数的性质... 当﹣2≤x≤1时，二次函数y=﹣（x﹣m）2+m2+1有最大值4，则实数m的值为（ ）
A. ﹣2 B.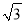 
或-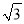
C. 2或-
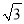D. 2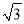或﹣
或-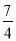
C
【解析】由题意得该抛物线的对称轴为x=m.
①当-2≤m≤1时,此时最大值为,即=4,
解得m= (舍去)或m=-;
②当m>1时,此时当x=1时,函数有最大值,所以,
解得m=2;
③当m<-2时,此时x=-2函数有最大值,所以,
解得m= (不合题意,舍去).
综上所述,m= -或m=2.
所以C选项是正确的. 海中有一个小岛A，它的周围a海里内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东75°方向上，航行12海里到达D点，这是测得小岛A在北偏东60°方向上．若渔船不改变航线继续向东航行而没有触礁危险，则a的最大值为（ ）
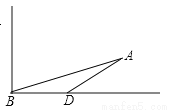
A. 5 B. 6 C. 6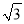
D. 8
B
【解析】试题分析：作AC⊥BD于点C， ∠ABD=90°-75°=15°，
∵∠ADC=90°-60°=30°， ∴∠BAD=∠ADC-∠ABD=30°-15°=15°，
∴∠ABD=∠BAD， ∴BD=AD=12（海里），
在直角△ADC中，AC=AD=×12=6（海里）．故选B． 如果一个多边形的内角和与它的外角和相等，那么这个多边形是____边形
四
【解析】∵多边形的外角和为360°，
而一个多边形的内角和与它的外角和正好相等，设这个多边形为n边形，
∴（n-2）•180°=360°，
∴n=4，
故答案为：四．