题目内容
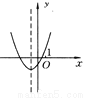
已知抛物线y=ax2+bx+c的大致图象如图所示,试确定a,b,c,b2-4ac及a+b+c的符号.
 a+b+c>0
【解析】分析:根据二次函数的图形确定a、b、c的符号,根据抛物线与x轴的交点确定的符号,由当x=1时,函数值的符号确定a+b+c的符号.
本题解析:
∵抛物线开口向上,∴a>0.∵抛物线与y轴的交点在y轴的负半轴上,∴C<0.又∵对称轴在y轴左侧,∴ab>0.∵a>0,∴b>0.∵抛物线与x轴有两个交点,∴△=b2-4ac>0.∵当x=1时,y>0,∴a+b+c>...
a+b+c>0
【解析】分析:根据二次函数的图形确定a、b、c的符号,根据抛物线与x轴的交点确定的符号,由当x=1时,函数值的符号确定a+b+c的符号.
本题解析:
∵抛物线开口向上,∴a>0.∵抛物线与y轴的交点在y轴的负半轴上,∴C<0.又∵对称轴在y轴左侧,∴ab>0.∵a>0,∴b>0.∵抛物线与x轴有两个交点,∴△=b2-4ac>0.∵当x=1时,y>0,∴a+b+c>...
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
抛物线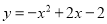 经过平移得到
经过平移得到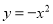 ,平移方法是( )
,平移方法是( )
A. 向右平移1个单位,再向上平移1个单位
B. 向右平移1个单位,再向下平移1个单位
C. 向左平移1个单位,再向上平移1个单位
D. 向左平移1个单位,再向下平移1个单位
 C
【解析】由抛物线得到顶点坐标为(1,-1),而平移后抛物线的顶点坐标为(0,0),根据顶点坐标的变化寻找平移方法为:向左平移1个单位,再向上平移1个单位.
故选:C.
C
【解析】由抛物线得到顶点坐标为(1,-1),而平移后抛物线的顶点坐标为(0,0),根据顶点坐标的变化寻找平移方法为:向左平移1个单位,再向上平移1个单位.
故选:C. 若二次函数y=ax2+bx+c的x与y的部分对应值如下表,则当x=1时,y的值为( )
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
A. -27
B. -13
C. -3
D. 5
 A
【解析】设二次函数的解析式为,
∵当x=-4或-2时,y=3,由抛物线的对称性可知h=-3,k=5,
∴,
把(-2,3)代入得,a=-2,
∴二次函数的解析式为,
当x=1时,y=-27.
故选:A.
A
【解析】设二次函数的解析式为,
∵当x=-4或-2时,y=3,由抛物线的对称性可知h=-3,k=5,
∴,
把(-2,3)代入得,a=-2,
∴二次函数的解析式为,
当x=1时,y=-27.
故选:A. 若分式方程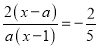 的解为x=3,则a的值为_______.
的解为x=3,则a的值为_______.
 5
【解析】由题意得: ,
解得:a=5,
经检验a=5符合原方程,
故答案为:5.
5
【解析】由题意得: ,
解得:a=5,
经检验a=5符合原方程,
故答案为:5. 若分式方程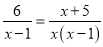 有增根,则增根是( )
有增根,则增根是( )
A. x=1 B. x=1或x=0 C. x=0 D. 不确定
 A
【解析】方程两边同乘x(x-1),得
6x=x+5,
解得:x=1,
检验:当x=1时,x(x-1)=0,所以x=1是原方程的增根,原方程无解,
故选A.
A
【解析】方程两边同乘x(x-1),得
6x=x+5,
解得:x=1,
检验:当x=1时,x(x-1)=0,所以x=1是原方程的增根,原方程无解,
故选A. 如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象的顶点p的横坐标是4,图象与x轴交于点A(m,0)和点B,且点A在点B的左侧,那么线段AB的长是____.(用含字母m的代数式表示)
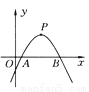
 8-2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4,
所以抛物线对称轴所在直线为x=4,交x轴于点D,
所以A.B两点关于对称轴对称,
因为点A(m,0),且m<4,即AD=4-m,
所以AB=2AD=2(4-m)=8-2m,
故答案为:8-2m.
8-2m
【解析】因为二次函数y=ax²+bx+c(a≠0)的图象的顶点P的横坐标是4,
所以抛物线对称轴所在直线为x=4,交x轴于点D,
所以A.B两点关于对称轴对称,
因为点A(m,0),且m<4,即AD=4-m,
所以AB=2AD=2(4-m)=8-2m,
故答案为:8-2m. 如果点(-2,-3)和(5,-3)都是抛物线y=ax2+bx+c上的点,那么抛物线的对称轴是 ( )
A. x=3 B. x=-3 C. x=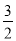 D. x=-
D. x=-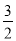
 C
【解析】点(?2,?3)和(5,?3)都是抛物线y=ax²+bx+c上的点,得
(?2,?3)、(5,?3)关于对称轴对称,
即对称轴过(?2,?3)、(5,?3)的中点,
x=,
故选C.
C
【解析】点(?2,?3)和(5,?3)都是抛物线y=ax²+bx+c上的点,得
(?2,?3)、(5,?3)关于对称轴对称,
即对称轴过(?2,?3)、(5,?3)的中点,
x=,
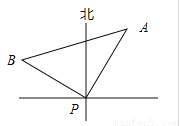
故选C. 某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行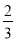 小时到达B处,那么tan∠BAP=( )
小时到达B处,那么tan∠BAP=( )
A. 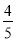 B.
B. 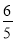 C.
C. 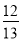 D.
D. 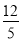
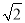
 A
【解析】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A.
A
【解析】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A. 一个多边形的每个外角都是36°,这个多边形是______边形
 十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十.
十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十. 
