题目内容
若分式方程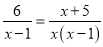
有增根，则增根是( )
A. x=1 B. x=1或x=0 C. x=0 D. 不确定
A
【解析】方程两边同乘x(x-1)，得
6x=x+5，
解得：x=1，
检验：当x=1时，x(x-1)=0，所以x=1是原方程的增根，原方程无解，
故选A.
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
直角坐标平面上将二次函数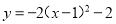
的图象向左平移1个单位，再向上平移1个单位，则其顶点为（ ）
A. （0，0）
B. （1，-2）
C. （0，-1）
D. （-2，1）
C
【解析】由题意得原抛物线的顶点为（1，-2），然后由图象向左平移1个单位，再向上平移1个单位，可得新抛物线的顶点为（0，-1）．
故选：C． 形状与抛物线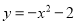
相同，对称轴是x=-2，且过点（0，3）的抛物线是（ ）
A.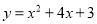 
B.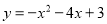 
C.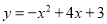 
D.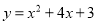 
或
D
【解析】设所求抛物线的函数关系式为，由抛物线过点（0，3），可得：c=3，
由抛物线形状与相同，
分为两种情况：①开口向下，则a＜0，
又∵对称轴x=-2，则x==-2．则b＜0，
由此可得出B选项符合题意．
②开口向下，则a＞0，
又∵对称轴x=-2，则x==-2．则b＞0，
由此可得出A选项符合题意，
综合上述，符合条件的是选项D．
... 当a＝_______时，方程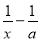
＝2的解为4．
【解析】由题意得： ，
解得：a=，
经检验a=符合原方程，
故答案为： . 方程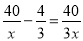
的解是______．
x=20
【解析】方程两边同时乘3x，得
120-4x=40，
解得：x=20，
检验：当x=20时，3x=60≠0，
所以x=20是原方程的根，
故答案为：x=20. 已知抛物线y＝ax2+bx+c的大致图象如图所示，试确定a，b，c，b2－4ac及a+b+c的符号．
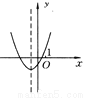
a＋b＋c＞0
【解析】分析:根据二次函数的图形确定a、b、c的符号,根据抛物线与x轴的交点确定的符号,由当x=1时,函数值的符号确定a+b+c的符号.
本题解析：
∵抛物线开口向上，∴a＞0．∵抛物线与y轴的交点在y轴的负半轴上，∴C＜0．又∵对称轴在y轴左侧，∴ab＞0．∵a＞0，∴b＞0．∵抛物线与x轴有两个交点，∴△＝b2－4ac＞0．∵当x=1时，y＞0，∴a＋b＋c＞... 已知二次函数的图象开口向上，且顶点在y轴的负半轴上，请你写出一个满足条件的二次函数的表达式________．
y=x2-2
【解析】依题意,只要满足二次项系数为正数,顶点坐标为(0,k),k<0即可,
根据顶点式写解析式,本题答案不唯一,如y=x²-2.故答案为：y=x2-2. 如图，甲、乙两船同时从港口O出发，其中甲船沿北偏西30°方向航行，乙船沿南偏西70°方向航行，已知两船的航行速度相同，如果1小时后甲、乙两船分别到达点A、B处，那么点B位于点A的（ ）
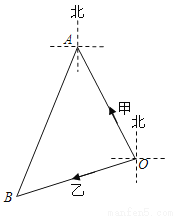
A. 南偏西40° B. 南偏西30° C. 南偏西20° D. 南偏西10°
C
【解析】试题分析：由甲船沿北偏西30°方向航行，乙船沿南偏西70°方向航行，得出∠BOA的度数，由两船的航行速度相同，得出AO=BO，得出∠BAO=50°，以及求出∠BAD的度数，得出点B位于点A的方向，故本题选C． 在四边形ABCD中,如果∠A:∠B:∠C:∠D=1:2:3:4,则∠D=______
144°
【解析】设∠A=x°，则∠B=2x°，∠C=3x°，∠D=4x°，
∵∠A+∠B+∠C+∠D=360°，
∴x+2x+3x+4x=360，
解得x=36°，
∴2x=72°，3x=108°，4x=144°，
所以∠A=36°，∠B=72°，∠C=108°，∠D=144°，
故答案为：144°.