题目内容
已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(1,4)和点(5,0),则该抛物线的解析式为__________.
 y=-0.5x+2x-2.5
【解析】∵抛物线对称轴是直线x=2且经过点A(5,0),
由抛物线的对称性可知:抛物线还经过点(?1,0),
设抛物线的解析式为y=a(x?x1)(x?x2)(a≠0),
即:y=a(x+1)(x?5),
把(1,4)代入得:4=?8a,
∴a=?.
∴抛物线的解析式为:y=?x2+2x+.
故答案为:y=?x2+2x+...
y=-0.5x+2x-2.5
【解析】∵抛物线对称轴是直线x=2且经过点A(5,0),
由抛物线的对称性可知:抛物线还经过点(?1,0),
设抛物线的解析式为y=a(x?x1)(x?x2)(a≠0),
即:y=a(x+1)(x?5),
把(1,4)代入得:4=?8a,
∴a=?.
∴抛物线的解析式为:y=?x2+2x+.
故答案为:y=?x2+2x+...
在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( )
A. 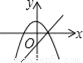 B.
B. 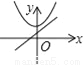 C.
C. 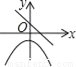 D.
D. 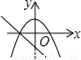
 D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D.
D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D. 与 形状相同的抛物线解析式为( )
形状相同的抛物线解析式为( )
A. y=
B. 
C. 
D. 
 D
【解析】抛物线的形状只与a有关,a相等,形状就相同,∴中,a=2.
故选:D.
D
【解析】抛物线的形状只与a有关,a相等,形状就相同,∴中,a=2.
故选:D. 分式方程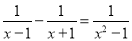 去分母时,两边都乘以________.
去分母时,两边都乘以________.
 (x+1)(x-1))
【解析】∵分式方程 可化为: ,
∴去分母时,方程两边应都乘以: .
(x+1)(x-1))
【解析】∵分式方程 可化为: ,
∴去分母时,方程两边应都乘以: . ―抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
 (1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析...
(1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析... 平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )
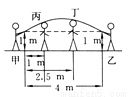
A. 1.5 m B. 1.625 m C. 1.66 m D. 1.67 m
 B
【解析】设所求的函数的解析式为y=ax2+bx+c,由已知,函数的图象过(-1,1),(0,1.5),(3,1)三点,易求其解析式为y=-x2+x+,∵丁头顶的横坐标为1.5,∴代入其解析式可求得其纵坐标为1.625m.故选B.
B
【解析】设所求的函数的解析式为y=ax2+bx+c,由已知,函数的图象过(-1,1),(0,1.5),(3,1)三点,易求其解析式为y=-x2+x+,∵丁头顶的横坐标为1.5,∴代入其解析式可求得其纵坐标为1.625m.故选B. 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: 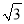 ≈1.732)
≈1.732)
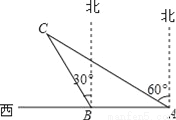
 17.
【解析】试题分析:过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
试题解析:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴...
17.
【解析】试题分析:过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
试题解析:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴... 如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )

A. 100 B. 200 C. 100 D. 200
B. 200 C. 100 D. 200
 B
【解析】试题分析:根据方位角可得:∠A=30°,∠CBA=120°,则∠C=30°,则△ABC为等腰三角形,故BC=AB=200m,故选B.
B
【解析】试题分析:根据方位角可得:∠A=30°,∠CBA=120°,则∠C=30°,则△ABC为等腰三角形,故BC=AB=200m,故选B. 四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数为( )
A. 80° B. 90° C. 170° D. 20°
 A
【解析】试题分析:四边形的内角和为360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°,
故选A.
A
【解析】试题分析:四边形的内角和为360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°,
故选A. 
