题目内容
―抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
 (1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析...
(1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析...
练习册系列答案
相关题目
若(2,5)、(4,5)是抛物线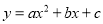 上的两个点则它的对称轴( )
上的两个点则它的对称轴( )
A. x=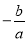 B.
B. 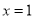 C.
C. 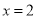 D.
D. 
 D
【解析】试题解析:因为点(2,5)、(4,5)在抛物线上,
根据抛物线上纵坐标相等的两点,其横坐标的平均数就是对称轴,
所以,对称轴
故选D.
D
【解析】试题解析:因为点(2,5)、(4,5)在抛物线上,
根据抛物线上纵坐标相等的两点,其横坐标的平均数就是对称轴,
所以,对称轴
故选D. 将二次函数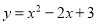 化为
化为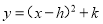 的形式,结果为( )
的形式,结果为( )
A. 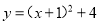
B. 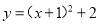
C. 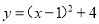
D. 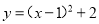
 D
【解析】
故选:D.
D
【解析】
故选:D. 如果方程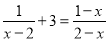 有增根, 那么增根是_______.
有增根, 那么增根是_______.
 x=2
【解析】∵原方程有增根,
∴最简公分母x-2=0,
解得x=2,
故答案为:x=2.
x=2
【解析】∵原方程有增根,
∴最简公分母x-2=0,
解得x=2,
故答案为:x=2. 下列关于x的方程中,不是分式方程的是( )
A. 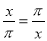 B.
B. 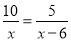 C.
C. 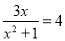 D.
D. 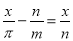
 D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
故选D.
D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
故选D. 已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(1,4)和点(5,0),则该抛物线的解析式为__________.
 y=-0.5x+2x-2.5
【解析】∵抛物线对称轴是直线x=2且经过点A(5,0),
由抛物线的对称性可知:抛物线还经过点(?1,0),
设抛物线的解析式为y=a(x?x1)(x?x2)(a≠0),
即:y=a(x+1)(x?5),
把(1,4)代入得:4=?8a,
∴a=?.
∴抛物线的解析式为:y=?x2+2x+.
故答案为:y=?x2+2x+...
y=-0.5x+2x-2.5
【解析】∵抛物线对称轴是直线x=2且经过点A(5,0),
由抛物线的对称性可知:抛物线还经过点(?1,0),
设抛物线的解析式为y=a(x?x1)(x?x2)(a≠0),
即:y=a(x+1)(x?5),
把(1,4)代入得:4=?8a,
∴a=?.
∴抛物线的解析式为:y=?x2+2x+.
故答案为:y=?x2+2x+... 二次函数y=ax2+bx+c满足b2=ac,且x=0时,y=﹣4,则( )
A. y最大=﹣4 B. y最小=﹣4 C. y最大=﹣3 D. y最小=﹣3
 C
【解析】试题分析:将x=0,y=-4代入可得:c=-4,根据可得: ,故函数有最大值,则最大值为: ,故选C.
C
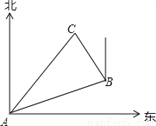
【解析】试题分析:将x=0,y=-4代入可得:c=-4,根据可得: ,故函数有最大值,则最大值为: ,故选C. 如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A. 北偏东20°方向上 B. 北偏西20°方向上
C. 北偏西30°方向上 D. 北偏西40°方向上
 B
【解析】试题分析:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,根据勾股定理的逆定理可知∠ABC=90°,根据平行线的性质可得:∠ABE=110°,则∠CBE=110°-90°=20°,即点C在点B的北偏西20°方向上.
B
【解析】试题分析:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,根据勾股定理的逆定理可知∠ABC=90°,根据平行线的性质可得:∠ABE=110°,则∠CBE=110°-90°=20°,即点C在点B的北偏西20°方向上. 若n边形的每个内角都等于150°,则n=_____.
 12
【解析】试题解析:由题意可得:
解得
故多边形是12边形.
故答案为:12.
12
【解析】试题解析:由题意可得:
解得
故多边形是12边形.
故答案为:12. 
