将二次函数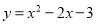
化成
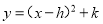形式，则h+k结果为（ ）
A. -5
B. 5
C. -3
D. 3
C
【解析】．
则h=1，k=-4，
∴h+k=-3．
故选：C． 抛物线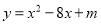
的顶点在x轴上，则m等于（ ）
A. -16
B. 16
C. -4
D. 8
B
【解析】抛物线的顶点纵坐标是： ，由顶点在x轴上，则
=0，
解得m=16．
故选：B． 用配方法将y=-2x2+4x+6化成y=a（x+h）2+k的形式，则a+h+k的值为（ ）
A. 5
B. 7
C. -1
D. -2
A
【解析】
∴a=-2，h=-1，k=8
∴a+h+k=-2+（-1）+8=5
故选：A． 关于抛物线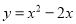
，下列说法正确的是（ ）
A. 顶点是坐标原点
B. 对称轴是直线x=2
C. 有最高点
D. 经过坐标原点
D
【解析】∵，
，
，
∴顶点坐标是：（1，-1），对称轴是直线x=1，
∵a=1＞0，∴开口向上，
有最小值，
∵当x=0时， ，
∴图象经过坐标原点，
故选：D． 如图，已知抛物线y=﹣x2+bx+c的对称轴为直线x=1，且与x轴的一个交点为（3，0），那么它对应的函数解析式是 ．
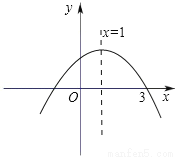
y=﹣x2+2x+3
【解析】
试题分析：∵抛物线y=﹣x2+bx+c的对称轴为直线x=1，
∴=1，解得b=2，
∵与x轴的一个交点为（3，0），
∴0=﹣9+6+c，
解得c=3，
故函数解析式为y=﹣x2+2x+3．
故答案为：y=﹣x2+2x+3 已知抛物线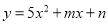
与x轴的交点为（
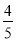，0）和（-2，0），则因式分解
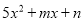的结果是__________
【解析】∵抛物线与x轴的交点为（，0）和（-2，0），a=5，
∴抛物线的解析式用交点式表示为
∴=
即： =．
故答案为： ． 把抛物线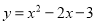
化为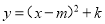
的形式，其中m，k为常数，则m-k=_________
5
【解析】，
∴m=1，k=-4，
∴m-k=1+4=5，
故答案为：5． 用一根长为80cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm2，一边长为xcm，则y与x的函数表达式为___________（化为一般式）
【解析】由题意得：矩形的另一边长=80÷2-x=40-x，
∴y=x（40-x）=．
故答案为：． 已知二次函数的图象经过原点及点（-2，-2），且图象与x轴的另一个交点到原点的距离为4，那么该二次函数的解析式为___________
或
【解析】∵图象与x轴的另一个交点到原点的距离为4，
∴这个交点坐标为（-4，0）、（4，0），
设二次函数解析式为，
①当这个交点坐标为（-4，0）时，
解得
所以二次函数解析式为
②当这个交点坐标为（4，0）时，
解得
所以二次函数解析式为
综上所述，二次函数解析式为或．
故答案为： 或 已知抛物线的顶点坐标为M（1，﹣2），且经过点N（2，3），求此二次函数的解析式．
y=5（x﹣1）2﹣2
【解析】试题分析：因为已知顶点坐标，所以可设抛物线顶点式： ，仅有一待定系数a，故只需找出图象上一个已知点，代入即可得到一个关于a的一元一次方程，解之，得a值，即可得到所求解析式.
【解析】
∵抛物线的顶点坐标为M（1，﹣2），
∴设此二次函数的解析式为y=a（x﹣1）2﹣2，
把点（2，3）代入解析式，得：
，
解得 a =5，
...