��Ŀ����
��֪�����ߵĶ�������ΪM��1����2�����Ҿ�����N��2��3������˶��κ����Ľ���ʽ��
 y=5��x��1��2��2
�������������������Ϊ��֪�������꣬���Կ��������߶���ʽ�� ������һ����ϵ��a����ֻ���ҳ�ͼ����һ����֪�㣬���뼴�ɵõ�һ������a��һԪһ�η��̣���֮����aֵ�����ɵõ��������ʽ.
��������
�������ߵĶ�������ΪM��1����2����
����˶��κ����Ľ���ʽΪy=a��x��1��2��2��
�ѵ㣨2��3���������ʽ���ã�
��
��� a =5��
...
y=5��x��1��2��2
�������������������Ϊ��֪�������꣬���Կ��������߶���ʽ�� ������һ����ϵ��a����ֻ���ҳ�ͼ����һ����֪�㣬���뼴�ɵõ�һ������a��һԪһ�η��̣���֮����aֵ�����ɵõ��������ʽ.
��������
�������ߵĶ�������ΪM��1����2����
����˶��κ����Ľ���ʽΪy=a��x��1��2��2��
�ѵ㣨2��3���������ʽ���ã�
��
��� a =5��
...
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д��۲����и�����ʽ������û�й���ʽ����( )
A. 2a+b��a+b B. 5m(a-b) ��-a+b
C. 3(a+b) ��-a-b D. 2x+2y��2
 A
��������ѡ��A��û�й���ʽ��ѡ��B���й���ʽa-b��ѡ��C���й���ʽa+b��ѡ��D���й���ʽ2.��ѡA.
A
��������ѡ��A��û�й���ʽ��ѡ��B���й���ʽa-b��ѡ��C���й���ʽa+b��ѡ��D���й���ʽ2.��ѡA. ���κ���y��x ²��x��m(mΪ����)��ͼ����ͼ��ʾ����x��aʱ��y��0����ô��x��a��1ʱ������ֵ�� ��
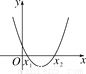
A. y��0 B. 0��y��m C. y��m D. y��m
 C
��������������������ݶԳ��ἰ����ֵ�ж�a��ȡֵ��Χ���Ӷ��ó�a��1��0����Ϊ��x��y��x���������С�����Ե�x=a��1��0ʱ������ֵyһ������m��
��������
��x=aʱ��y��0��
��a�ķ�Χ��x1��a��x2��
�ֶԳ�����x=��
����a��1��0��
��x��y��x�����������
��x=0�Ǻ���ֵ��m��
�����x=a��1��0ʱ������ֵyһ������m��
...
C
��������������������ݶԳ��ἰ����ֵ�ж�a��ȡֵ��Χ���Ӷ��ó�a��1��0����Ϊ��x��y��x���������С�����Ե�x=a��1��0ʱ������ֵyһ������m��
��������
��x=aʱ��y��0��
��a�ķ�Χ��x1��a��x2��
�ֶԳ�����x=��
����a��1��0��
��x��y��x�����������
��x=0�Ǻ���ֵ��m��
�����x=a��1��0ʱ������ֵyһ������m��
... ��������y=ax2+bx+c(a��0)����A(0��2)��B(4��3)��C���㣬���е�C��ֱ��x=2�ϣ��ҵ�C�������ߵĶԳ���ľ������1���������ߵĺ�������ʽΪ______.
 y=x2-x+2��y=-x2+x+2.
������������������������߹�A(0��2)����.
�������߹�B(4��3)����.
�������߹�C���ҵ�C��ֱ���ϣ���C�������߶Գ���ľ������1��
��.
���û�.
�������ߵĺ�������ʽΪ��.
y=x2-x+2��y=-x2+x+2.
������������������������߹�A(0��2)����.
�������߹�B(4��3)����.
�������߹�C���ҵ�C��ֱ���ϣ���C�������߶Գ���ľ������1��
��.
���û�.
�������ߵĺ�������ʽΪ��. ���κ���y=-x2+bx+c��ͼ�����ߵ���(-1��-3)����b��c��ֵ�ֱ���( )
A. b=2��c=4 B. b=2��c=-4 C. b=-2��c=4 D. b=-2��c=-4
 D
���������������������ɵú������������ǣ�-1��-3�����ԶԳ�����x=-1,�Գ���x=,a=-1,����b=-2,���㣨-1��-3���������ʽ��c=-4,���Ժ�������ʽΪy=-x2-2x-4,��b=-2,c=-4,��ѡD.
D
���������������������ɵú������������ǣ�-1��-3�����ԶԳ�����x=-1,�Գ���x=,a=-1,����b=-2,���㣨-1��-3���������ʽ��c=-4,���Ժ�������ʽΪy=-x2-2x-4,��b=-2,c=-4,��ѡD. ��ͼ����֪������y=��x2+bx+c�ĶԳ���Ϊֱ��x=1������x���һ������Ϊ��3��0������ô����Ӧ�ĺ�������ʽ��������
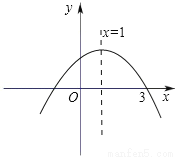
 y=��x2+2x+3
��������
�����������������y=��x2+bx+c�ĶԳ���Ϊֱ��x=1��
��=1�����b=2��
����x���һ������Ϊ��3��0����
��0=��9+6+c��
���c=3��
�ʺ�������ʽΪy=��x2+2x+3��
�ʴ�Ϊ��y=��x2+2x+3
y=��x2+2x+3
��������
�����������������y=��x2+bx+c�ĶԳ���Ϊֱ��x=1��
��=1�����b=2��
����x���һ������Ϊ��3��0����
��0=��9+6+c��
���c=3��
�ʺ�������ʽΪy=��x2+2x+3��
�ʴ�Ϊ��y=��x2+2x+3 һ�����κ�����ͼ����A��0��0����B��-1��-11����C��1��9�����㣬��������κ����Ĺ�ϵʽ�ǣ�������
A. 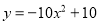
B. 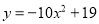
C. 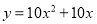
D. 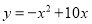
 D
�����������������߾���ԭ�㣬��������亯����ϵʽΪ��
��B��C����������룬��
���
������ϵʽΪ
��ѡ��D��
D
�����������������߾���ԭ�㣬��������亯����ϵʽΪ��
��B��C����������룬��
���
������ϵʽΪ
��ѡ��D�� ��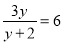 ����
����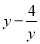 =_______.
=_______.
 -3
���������ⷽ�̣��ã�y=-4��������y=-4�Ƿ��̵Ľ⣬
����=-4+1=-3��
�ʴ�Ϊ��-3.
-3
���������ⷽ�̣��ã�y=-4��������y=-4�Ƿ��̵Ľ⣬
����=-4+1=-3��
�ʴ�Ϊ��-3. �����д��ڶ����غ����ļ���������̨��Ϯ����һ�Σ���������ֲ��̨��������������A����������300ǧ��B������ͼ������ÿСʱ10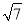 ǧ���ٶ���ƫ��30���BC�����ƶ�������̨���������ƶ������У�������A���ܵ�Ӱ�죬�Ҿ�̨������200ǧ�ķ�Χ����̨������Ӱ���������Ӱ��������A��ʱ�����������������
ǧ���ٶ���ƫ��30���BC�����ƶ�������̨���������ƶ������У�������A���ܵ�Ӱ�죬�Ҿ�̨������200ǧ�ķ�Χ����̨������Ӱ���������Ӱ��������A��ʱ�����������������
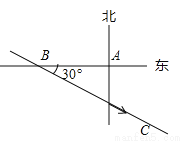
A. 5 B. 6 C. 8 D. 10
 D
���������������������A��AD��BC��D���������AB=300����ABD��30�㣬��AD =150��km����
�����е�A�ܵ�̨������Ӱ�����̨���ľ�A��200km�����պô���BC�ϵ�E��F����
����Rt��ADE��AE��200��AD��150 ��DE=50km�� ��EF=2DE=100km��
��t=100��10=10h����ѡD��
D
���������������������A��AD��BC��D���������AB=300����ABD��30�㣬��AD =150��km����
�����е�A�ܵ�̨������Ӱ�����̨���ľ�A��200km�����պô���BC�ϵ�E��F����
����Rt��ADE��AE��200��AD��150 ��DE=50km�� ��EF=2DE=100km��
��t=100��10=10h����ѡD�� 
