在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( )
A. 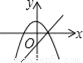 B.
B. 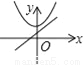 C.
C. 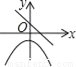 D.
D. 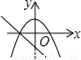
 D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D.
D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D. 如图图形中,阴影部分面积相等的是( )

A. 甲 乙
B. 甲 丙
C. 乙 丙
D. 丙 丁
 B
【解析】根据题意,可知:
甲:直线与x轴交点为(3,0),与y轴的交点为(0,4),则阴影部分的面积为×3×4=6;
乙:阴影部分为斜边为4的等腰直角三角形,其面积为×4×2=4;
丙:抛物线与x轴的两个交点为(-3,0)与(3,0),顶点坐标为(0,-2),则阴影部分的面积为×6×2=6;
丁:此函数是反比例函数,那么阴影部分的面积为×6=3;
因此甲、丙...
B
【解析】根据题意,可知:
甲:直线与x轴交点为(3,0),与y轴的交点为(0,4),则阴影部分的面积为×3×4=6;
乙:阴影部分为斜边为4的等腰直角三角形,其面积为×4×2=4;
丙:抛物线与x轴的两个交点为(-3,0)与(3,0),顶点坐标为(0,-2),则阴影部分的面积为×6×2=6;
丁:此函数是反比例函数,那么阴影部分的面积为×6=3;
因此甲、丙... 王芳将如图所示的三条水平直线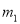 ,
, 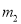 ,
, 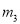 的其中一条记为x轴(向右为正方向),三条竖直直线
的其中一条记为x轴(向右为正方向),三条竖直直线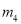 ,
, 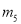 ,
, 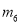 的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线
的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线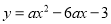 ,则她所选择的x轴和y轴分别为( )
,则她所选择的x轴和y轴分别为( )
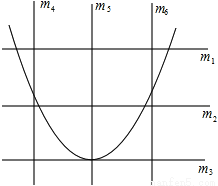
A. 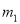 ,
, 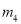
B. 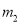 ,
, 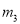
C. 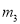 ,
, 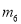
D. 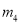 ,
, 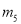
 A
【解析】根据抛物线开口向上可知a>0,将抛物线配方为,可得抛物线的对称轴为x=3,可知应选择的y轴为直线;由顶点坐标为(3,-3-9a),抛物线与y轴的交点为(0,-3),而-3-9a<-3,可知应选择的x轴为直线,
故选:A.
A
【解析】根据抛物线开口向上可知a>0,将抛物线配方为,可得抛物线的对称轴为x=3,可知应选择的y轴为直线;由顶点坐标为(3,-3-9a),抛物线与y轴的交点为(0,-3),而-3-9a<-3,可知应选择的x轴为直线,
故选:A. 已知抛物线y=ax2+bx+c开口向下,顶点坐标(3,-5),那么该抛物线有( )
A. 最小值-5
B. 最大值-5
C. 最小值3
D. 最大值3
 B
【解析】由抛物线的开口向下和其顶点坐标为(3,-5),根据抛物线的性质,可以知该抛物线有最大值-5.
故选:B.
B
【解析】由抛物线的开口向下和其顶点坐标为(3,-5),根据抛物线的性质,可以知该抛物线有最大值-5.
故选:B. 抛物线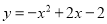 经过平移得到
经过平移得到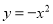 ,平移方法是( )
,平移方法是( )
A. 向右平移1个单位,再向上平移1个单位
B. 向右平移1个单位,再向下平移1个单位
C. 向左平移1个单位,再向上平移1个单位
D. 向左平移1个单位,再向下平移1个单位
 C
【解析】由抛物线得到顶点坐标为(1,-1),而平移后抛物线的顶点坐标为(0,0),根据顶点坐标的变化寻找平移方法为:向左平移1个单位,再向上平移1个单位.
故选:C.
C
【解析】由抛物线得到顶点坐标为(1,-1),而平移后抛物线的顶点坐标为(0,0),根据顶点坐标的变化寻找平移方法为:向左平移1个单位,再向上平移1个单位.
故选:C. 若(2,5)、(4,5)是抛物线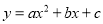 上的两个点则它的对称轴( )
上的两个点则它的对称轴( )
A. x=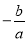 B.
B. 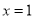 C.
C. 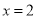 D.
D. 
 D
【解析】试题解析:因为点(2,5)、(4,5)在抛物线上,
根据抛物线上纵坐标相等的两点,其横坐标的平均数就是对称轴,
所以,对称轴
故选D.
D
【解析】试题解析:因为点(2,5)、(4,5)在抛物线上,
根据抛物线上纵坐标相等的两点,其横坐标的平均数就是对称轴,
所以,对称轴
故选D. 若点A(2,  ),B(-3,
),B(-3, 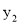 ),C(-1,
),C(-1, 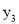 )三点在抛物线
)三点在抛物线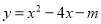 的图象上,则
的图象上,则 、
、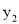 、
、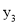 的大小关系是( )
的大小关系是( )
A. 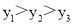
B. 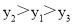
C. 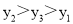
D. 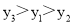
 C
【解析】首先求出二次函数的图象的对称轴x==2,且由a=1>0,可知其开口向上,然后由A(2, )中x=2,知最小,再由B(-3, ),C(-1, )都在对称轴的左侧,而在对称轴的左侧,y随x得增大而减小,所以.总结可得.
故选:C.
C
【解析】首先求出二次函数的图象的对称轴x==2,且由a=1>0,可知其开口向上,然后由A(2, )中x=2,知最小,再由B(-3, ),C(-1, )都在对称轴的左侧,而在对称轴的左侧,y随x得增大而减小,所以.总结可得.
故选:C. 若函数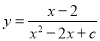 的自变量x的取值范围是全体实数,则c的取值范围是( )
的自变量x的取值范围是全体实数,则c的取值范围是( )
A. c>1
B. c=1
C. c<1
D. c≤1
 A
【解析】先根据分式的意义,分母不等于0,得出,再根据二次函数(a≠0)的图象性质,可知当二次项系数a>0,△=时,有y>0,此时自变量x的取值范围是全体实数,解得c>1.
故选:A.
A
【解析】先根据分式的意义,分母不等于0,得出,再根据二次函数(a≠0)的图象性质,可知当二次项系数a>0,△=时,有y>0,此时自变量x的取值范围是全体实数,解得c>1.
故选:A. 二次函数y=x ²-x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a-1时,函数值( )
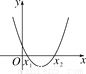
A. y<0 B. 0<y<m C. y>m D. y=m
 C
【解析】试题分析:根据对称轴及函数值判断a的取值范围,从而得出a﹣1<0,因为当x是y随x的增大而减小,所以当x=a﹣1<0时,函数值y一定大于m.
【解析】
当x=a时,y<0,
则a的范围是x1<a<x2,
又对称轴是x=,
所以a﹣1<0,
当x是y随x的增大而减小,
当x=0是函数值是m.
因而当x=a﹣1<0时,函数值y一定大于m.
...
C
【解析】试题分析:根据对称轴及函数值判断a的取值范围,从而得出a﹣1<0,因为当x是y随x的增大而减小,所以当x=a﹣1<0时,函数值y一定大于m.
【解析】
当x=a时,y<0,
则a的范围是x1<a<x2,
又对称轴是x=,
所以a﹣1<0,
当x是y随x的增大而减小,
当x=0是函数值是m.
因而当x=a﹣1<0时,函数值y一定大于m.
... 直角坐标平面上将二次函数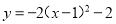 的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )
的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )
A. (0,0)
B. (1,-2)
C. (0,-1)
D. (-2,1)
 C
【解析】由题意得原抛物线的顶点为(1,-2),然后由图象向左平移1个单位,再向上平移1个单位,可得新抛物线的顶点为(0,-1).
故选:C.
C
【解析】由题意得原抛物线的顶点为(1,-2),然后由图象向左平移1个单位,再向上平移1个单位,可得新抛物线的顶点为(0,-1).
故选:C.