题目内容
如图图形中，阴影部分面积相等的是（ ）
A. 甲 乙
B. 甲 丙
C. 乙 丙
D. 丙 丁
B
【解析】根据题意，可知：
甲：直线与x轴交点为（3，0），与y轴的交点为（0，4），则阴影部分的面积为×3×4=6；
乙：阴影部分为斜边为4的等腰直角三角形，其面积为×4×2=4；
丙：抛物线与x轴的两个交点为（-3，0）与（3，0），顶点坐标为（0，-2），则阴影部分的面积为×6×2=6；
丁：此函数是反比例函数，那么阴影部分的面积为×6=3；
因此甲、丙...
练习册系列答案
相关题目
如果水流的速度为a m/min(定量)，那么每分钟的进水量Q(m3)与所选择的水管直径D(m)之间的函数关系式是什么?
Q＝.
【解析】试题分析：根据圆柱体的体积公式V=πr2h，直接代入求解即可.
试题解析：函数关系式为Q＝a·π·()2＝ . 把一个多项式化成几个________的_______的形式，叫做把这个多项式分解因式.
整式 积
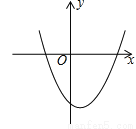
【解析】根据因式分解的定义可得：把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式. 已知二次函数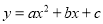
的图象如图所示，则点P（a，bc）在第_______象限．
一
【解析】从图象得出，二次函数的对称轴在y轴的右侧，且开口向上，可得a＞0， ＞0，所以b＜0，然后由二次函数的图象与y轴交于y轴的负半轴，得c＜0，即可得到a＞0，bc＞0，则点P（a，bc）在第一象限．
故答案为：一． 若点A（2， 
），B（-3，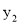 
），C（-1， 
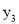）三点在抛物线
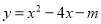的图象上，则
、
、
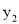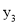的大小关系是（ ）
A.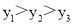 
B.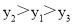 
C.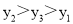 
D.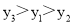 
C
【解析】首先求出二次函数的图象的对称轴x==2，且由a=1＞0，可知其开口向上，然后由A（2， ）中x=2，知最小，再由B（-3， ），C（-1， ）都在对称轴的左侧，而在对称轴的左侧，y随x得增大而减小，所以．总结可得．
故选：C． 抛物线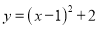
的顶点坐标是（ ）
A. （-1，2） B. （-1，-2） C. （1，2） D. （1，-2）
C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y=（x-1）2+2的顶点坐标是（1，2）．
故选：C． 将二次函数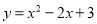
化为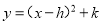
的形式，结果为（ ）
A.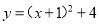 
B.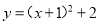 
C. 
D. 
D
【解析】
故选：D． 用配方法将y=-2x2+4x+6化成y=a（x+h）2+k的形式，则a+h+k的值为（ ）
A. 5
B. 7
C. -1
D. -2
A
【解析】
∴a=-2，h=-1，k=8
∴a+h+k=-2+（-1）+8=5
故选：A． 用配方法把二次函数y＝l+2x－x2化为y＝a(x－h)2+k的形式，作出它的草图，回答下列问题．
(1)求抛物线的顶点坐标和它与x轴的交点坐标；
(2)当x取何值时，y随x的增大而增大?
(3)当x取何值时，y的值大于0?
y=－(x－1)2＋2(1)顶点坐标为(1，2)，与x轴的两个交点坐标分别为(1－，0)，(1＋，0)(2)当x＜1时，y随x的增大而增大.(3)当l－＜x＜1＋时，y的值大于0
【解析】分析：（1）利用配方法得到y=-(x-1)²+2，则根据二次函数的性质可得到抛物线的顶点坐标；再利用抛物线与x轴的交点问题，通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标；（2）根据二次函数的性质...