题目内容
二次函数y=x ²-x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a-1时,函数值( )
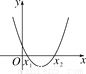
A. y<0 B. 0<y<m C. y>m D. y=m
 C
【解析】试题分析:根据对称轴及函数值判断a的取值范围,从而得出a﹣1<0,因为当x是y随x的增大而减小,所以当x=a﹣1<0时,函数值y一定大于m.
【解析】
当x=a时,y<0,
则a的范围是x1<a<x2,
又对称轴是x=,
所以a﹣1<0,
当x是y随x的增大而减小,
当x=0是函数值是m.
因而当x=a﹣1<0时,函数值y一定大于m.
...
C
【解析】试题分析:根据对称轴及函数值判断a的取值范围,从而得出a﹣1<0,因为当x是y随x的增大而减小,所以当x=a﹣1<0时,函数值y一定大于m.
【解析】
当x=a时,y<0,
则a的范围是x1<a<x2,
又对称轴是x=,
所以a﹣1<0,
当x是y随x的增大而减小,
当x=0是函数值是m.
因而当x=a﹣1<0时,函数值y一定大于m.
...
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
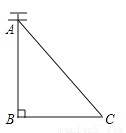
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A. 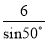 B.
B. 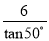 C. 6cos50° D.
C. 6cos50° D. 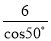
 D
【解析】试题分析:根据Rt△ABC中∠C的余弦值可得:cos50°=,则AC=,故选D.
D
【解析】试题分析:根据Rt△ABC中∠C的余弦值可得:cos50°=,则AC=,故选D. 把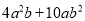 分解因式时,应提取的公因式是____________.
分解因式时,应提取的公因式是____________.
 2ab
【解析】把分解因式时,应提取的公因式是2ab.
2ab
【解析】把分解因式时,应提取的公因式是2ab. 如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[2,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[4,2],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[2,4]?
 (1)此函数图象的顶点坐标为:(1,0);(2)图象对应的函数的特征数为:[0,﹣1];(3)原函数的图象向右平移1个单位,再向上平移5个单位得到.
【解析】试题分析:(1)根据特征数的定义,得二次函数为y=x2﹣2x+1,再利用配方得:y=(x﹣1)2,从而顶点坐标为(1,0)
(2)①根据特征数的定义,得二次函数为y=x2+2x-1,再利用配方得y=(x+1)2﹣2,图象先向右平移...
(1)此函数图象的顶点坐标为:(1,0);(2)图象对应的函数的特征数为:[0,﹣1];(3)原函数的图象向右平移1个单位,再向上平移5个单位得到.
【解析】试题分析:(1)根据特征数的定义,得二次函数为y=x2﹣2x+1,再利用配方得:y=(x﹣1)2,从而顶点坐标为(1,0)
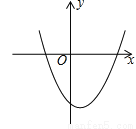
(2)①根据特征数的定义,得二次函数为y=x2+2x-1,再利用配方得y=(x+1)2﹣2,图象先向右平移... 已知二次函数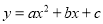 的图象如图所示,则点P(a,bc)在第_______象限.
的图象如图所示,则点P(a,bc)在第_______象限.
 一
【解析】从图象得出,二次函数的对称轴在y轴的右侧,且开口向上,可得a>0, >0,所以b<0,然后由二次函数的图象与y轴交于y轴的负半轴,得c<0,即可得到a>0,bc>0,则点P(a,bc)在第一象限.
故答案为:一.
一
【解析】从图象得出,二次函数的对称轴在y轴的右侧,且开口向上,可得a>0, >0,所以b<0,然后由二次函数的图象与y轴交于y轴的负半轴,得c<0,即可得到a>0,bc>0,则点P(a,bc)在第一象限.
故答案为:一. 已知抛物线y=ax2+bx+c开口向下,顶点坐标(3,-5),那么该抛物线有( )
A. 最小值-5
B. 最大值-5
C. 最小值3
D. 最大值3
 B
【解析】由抛物线的开口向下和其顶点坐标为(3,-5),根据抛物线的性质,可以知该抛物线有最大值-5.
故选:B.
B
【解析】由抛物线的开口向下和其顶点坐标为(3,-5),根据抛物线的性质,可以知该抛物线有最大值-5.
故选:B. 抛物线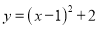 的顶点坐标是( )
的顶点坐标是( )
A. (-1,2) B. (-1,-2) C. (1,2) D. (1,-2)
 C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是(h,k),可知抛物线y=(x-1)2+2的顶点坐标是(1,2).
故选:C.
C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是(h,k),可知抛物线y=(x-1)2+2的顶点坐标是(1,2).
故选:C. 已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.
 y=5(x﹣1)2﹣2
【解析】试题分析:因为已知顶点坐标,所以可设抛物线顶点式: ,仅有一待定系数a,故只需找出图象上一个已知点,代入即可得到一个关于a的一元一次方程,解之,得a值,即可得到所求解析式.
【解析】
∵抛物线的顶点坐标为M(1,﹣2),
∴设此二次函数的解析式为y=a(x﹣1)2﹣2,
把点(2,3)代入解析式,得:
,
解得 a =5,
...
y=5(x﹣1)2﹣2
【解析】试题分析:因为已知顶点坐标,所以可设抛物线顶点式: ,仅有一待定系数a,故只需找出图象上一个已知点,代入即可得到一个关于a的一元一次方程,解之,得a值,即可得到所求解析式.
【解析】
∵抛物线的顶点坐标为M(1,﹣2),
∴设此二次函数的解析式为y=a(x﹣1)2﹣2,
把点(2,3)代入解析式,得:
,
解得 a =5,
... 某煤矿原计划x天生存120t煤,由于采用新的技术,每天增加生存3t,因此提前2天完成,列出的方程为( )
A. 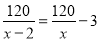 B.
B. 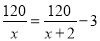
C. 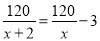 D.
D. 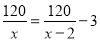
 D
【解析】因为原计划x天生产120吨煤,所以原计划每天生产吨,因为采取新的技术,提前2天 ,所以现在每天生产吨,因为现在每天比原计划每天增加3吨,所以可列方程是,故选D.
D
【解析】因为原计划x天生产120吨煤,所以原计划每天生产吨,因为采取新的技术,提前2天 ,所以现在每天生产吨,因为现在每天比原计划每天增加3吨,所以可列方程是,故选D. 
