题目内容
若(2,5)、(4,5)是抛物线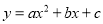 上的两个点则它的对称轴( )
上的两个点则它的对称轴( )
A. x=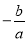 B.
B. 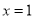 C.
C. 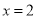 D.
D. 
 D
【解析】试题解析:因为点(2,5)、(4,5)在抛物线上,
根据抛物线上纵坐标相等的两点,其横坐标的平均数就是对称轴,
所以,对称轴
故选D.
D
【解析】试题解析:因为点(2,5)、(4,5)在抛物线上,
根据抛物线上纵坐标相等的两点,其横坐标的平均数就是对称轴,
所以,对称轴
故选D.
练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
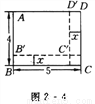
如图2 - 4所示,长方形ABCD的长为5 cm,宽为4 cm,如果将它的长和宽都减去x(cm),那么它剩下的小长方形AB′C′D′的面积为y(cm2).
(1)写出y与x的函数关系式;
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
 (1) y=x2-9x+20;(2) 二次函数;(3) 0<x<4.
【解析】试题分析:(1)根据长方形的面积公式,根据图示求解即可得到函数关系式;
(2)通过二次函数的定义可判断;
(3)根据x取值不能大于原方程的长方形的宽进行分析.
试题解析:(1)根据长方形的面积公式,得y=(5-x)·(4-x)=x2-9x+20,所以y与x的函数关系式为y=x2-9x+20.
...
(1) y=x2-9x+20;(2) 二次函数;(3) 0<x<4.
【解析】试题分析:(1)根据长方形的面积公式,根据图示求解即可得到函数关系式;
(2)通过二次函数的定义可判断;
(3)根据x取值不能大于原方程的长方形的宽进行分析.
试题解析:(1)根据长方形的面积公式,得y=(5-x)·(4-x)=x2-9x+20,所以y与x的函数关系式为y=x2-9x+20.
... 下列由左到右的变形中,哪些是分解因式?哪些不是?请说出理由.
(1)a(x+y)=ax+ay;
(2)x2+2xy+y2-1=x(x+2y)+(y +1)(y-1);
(3)ax2-9a=a(x+3)(x-3);
(4)x2+2+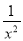 =
=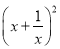
(5)2a3=2a·a·a.
 见解析
【解析】试题分析:根据因式分解的定义判断即可.
试题解析:
因为(1) (2)的右边都不是整式的积的形式.所以它们不是分解因式;(4)中, 都不是整式,(5)中的2a3不是多项式,所以它们也不是分解因式.只有(3)的左边是多项式,右边是整式的积的形式,所以(3)是分解因式.
见解析
【解析】试题分析:根据因式分解的定义判断即可.
试题解析:
因为(1) (2)的右边都不是整式的积的形式.所以它们不是分解因式;(4)中, 都不是整式,(5)中的2a3不是多项式,所以它们也不是分解因式.只有(3)的左边是多项式,右边是整式的积的形式,所以(3)是分解因式. 用配方法把函数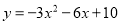 化成
化成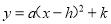 的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.
的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.
 向下,x=-1,(-1,13),最大值13
【解析】试题分析:根据这个函数的二次项系数是-3,配方法变形成的形式,直接可判断出开口方向,对称轴,顶点坐标和最值.
试题解析:∵,
∴开口向下,对称轴x=-1,顶点坐标(-1,13),最大值13.
向下,x=-1,(-1,13),最大值13
【解析】试题分析:根据这个函数的二次项系数是-3,配方法变形成的形式,直接可判断出开口方向,对称轴,顶点坐标和最值.
试题解析:∵,
∴开口向下,对称轴x=-1,顶点坐标(-1,13),最大值13. 便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足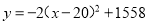 ,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )
,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )
A. 20 B. 1508 C. 1558 D. 1585
 C
【解析】由题意知,一周利润y(元)与每件销售价x(元)之间的关系满足,且15≤x≤22,根据二次函数的开口方向向下,可知当x=20时, .
故选:C.
C
【解析】由题意知,一周利润y(元)与每件销售价x(元)之间的关系满足,且15≤x≤22,根据二次函数的开口方向向下,可知当x=20时, .
故选:C. 在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( )
A. 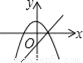 B.
B. 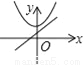 C.
C. 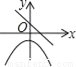 D.
D. 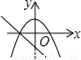
 D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D.
D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D. 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
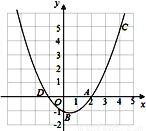
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
 (1)y=x2-x-1; (2)(-1,0);(3)见图象
【解析】(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
【解析】
(1)...
(1)y=x2-x-1; (2)(-1,0);(3)见图象
【解析】(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
【解析】
(1)... 把抛物线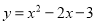 化为
化为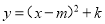 的形式,其中m,k为常数,则m-k=_________
的形式,其中m,k为常数,则m-k=_________
 5
【解析】,
∴m=1,k=-4,
∴m-k=1+4=5,
故答案为:5.
5
【解析】,
∴m=1,k=-4,
∴m-k=1+4=5,
故答案为:5. ―抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
 (1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析...
(1) y=2x2+2x-4(2)(-,- )
【解析】分析:(1)因为已知抛物线与x轴两交点坐标,则设交点式y=a(x+2)(x-1,然后把c(2,8代入求出a即可;(2)把(1)中的函数解析式转化为顶点式,可以直接得到答案.
本题解析:
(1)设这个抛物线的解析式为y=ax2+bx+c.将A(-2,0),B(1,0),C(2,8)三点代入,得解这个方程组,得∴所求抛物线的解析... 
