题目内容
若点A（2， 
），B（-3， 
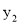），C（-1， 
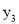）三点在抛物线
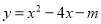的图象上，则
、
、
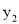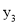的大小关系是（ ）
A.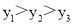 
B.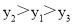 
C.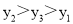 
D.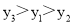 
C
【解析】首先求出二次函数的图象的对称轴x==2，且由a=1＞0，可知其开口向上，然后由A（2， ）中x=2，知最小，再由B（-3， ），C（-1， ）都在对称轴的左侧，而在对称轴的左侧，y随x得增大而减小，所以．总结可得．
故选：C．
红果子三级测试卷系列答案
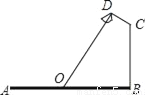
课堂练加测系列答案如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）
A. （11﹣2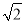
）米 B. （11
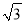﹣2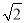
）米 C. （11﹣2
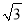）米 D. （11
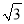﹣4）米
D
【解析】试题解析：如图，延长OD，BC交于点P．
∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，
∴在直角△CPD中，DP=DC•cot30°=2m，PC=CD÷（sin30°）=4米，
∵∠P=∠P，∠PDC=∠B=90°，
∴△PDC∽△PBO，
∴，
∴PB=米，
∴BC=PB-PC=米．
故选B． 若关于x的多项式3x2+mx+n分解因式的结果为(3x+2)(x-1)，求m、n的值.
m=-1,n=-2.
【解析】试题分析：把(3x+2)(x-1)利用多项式乘以多项式的法则展开，与多项式3x2+mx+n比较，即可得m、n的值.
试题解析：
由题意可得：(3x+2)(x-1)=3x2+2x-3x-2=3x2-x-2=3x2+mx+n，
所以m=-1,n=-2. 已知m，n是关于x的方程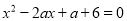
的两实根，求
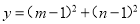的最小值．
8
【解析】试题分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把整理成m+n与mn的形式，代入进行计算求解．
试题解析：依题意△=≥0，
即，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
即
=
=
=，
∴a=3时，y的最小值为8．
故答案为：8． 已知二次函数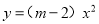
的图象开口向下，则m的取值范围是________
m＜2
【解析】由二次函数的图象的开口方向，知m-2＜0，确定m的取值范围m＜2．
故答案为：m＜2． 如图图形中，阴影部分面积相等的是（ ）
A. 甲 乙
B. 甲 丙
C. 乙 丙
D. 丙 丁
B
【解析】根据题意，可知：
甲：直线与x轴交点为（3，0），与y轴的交点为（0，4），则阴影部分的面积为×3×4=6；
乙：阴影部分为斜边为4的等腰直角三角形，其面积为×4×2=4；
丙：抛物线与x轴的两个交点为（-3，0）与（3，0），顶点坐标为（0，-2），则阴影部分的面积为×6×2=6；
丁：此函数是反比例函数，那么阴影部分的面积为×6=3；
因此甲、丙... 如图，抛物线
与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
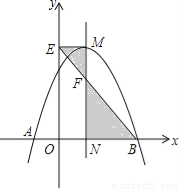
（1），（1，4）；（2）.
【解析】试题分析：（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标.
（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．
试题解析：【解析】
（1）∵点A在抛物线上，
∴，解得：c=3，
∴抛物线的解析式为.
∵，
∴抛物线的顶点M（1，4）；
（2）∵A（﹣1，0），抛物... 用一根长为80cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm2，一边长为xcm，则y与x的函数表达式为___________（化为一般式）
【解析】由题意得：矩形的另一边长=80÷2-x=40-x，
∴y=x（40-x）=．
故答案为：． 如图所示，矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上，边OC在y轴正半轴上)绕点B逆时针旋转得到的．点O′在x轴的正半轴上，点B的坐标为(1，3)．
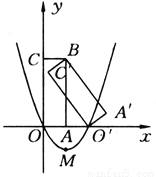
(1)如果二次函数y＝ax2+bx+c（a≠0)的图象经过O，O′两点，且图象顶点M的纵坐标为－l，求这个二次函数的解析式；
(2)在(1)中求出的二次函数图象对称轴的右侧，是否存在点P，使得△POM为直角三角形?若存在，求出点P的坐标和△POM的面积；若不存在，请说明理由；
(3)求边C′O′所在直线的解析式．
(1) y＝x2－2x(2)1(3)y=
【解析】分析:(1)连接BO,B则B0=B,求出M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知 (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析：(1)如图2－83所示，连...