便民商店经营一种商品，在销售过程中，发现一周利润y（元）与每件销售价x（元）之间的关系满足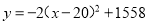
，由于某种原因，价格只能15≤x≤22，那么一周可获得最大利润是（ ）
A. 20 B. 1508 C. 1558 D. 1585
C
【解析】由题意知，一周利润y（元）与每件销售价x（元）之间的关系满足，且15≤x≤22，根据二次函数的开口方向向下，可知当x=20时， ．
故选：C． 已知二次函数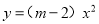
的图象开口向下，则m的取值范围是________
m＜2
【解析】由二次函数的图象的开口方向，知m-2＜0，确定m的取值范围m＜2．
故答案为：m＜2． 黄冈中学是百年名校，百年校庆上的焰火晚会令很多人记忆犹新．有一种焰火升高高度为h（m）与飞行时间t（s）的关系式是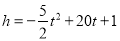
，若这种焰火在点燃升空后到最高处引爆，则从点火到引爆所需时间为__________s．
4
【解析】根据关系式可知焰火的运行轨迹是一个开口向下的抛物线，已知焰火在升到最高时引爆，即到达抛物线的顶点时引爆，顶点横坐标就是从点火到引爆所需时间．则t==4s，
故答案为：4． 已知二次函数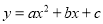
的图象如图所示，则点P（a，bc）在第_______象限．
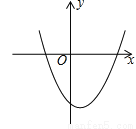
一
【解析】从图象得出，二次函数的对称轴在y轴的右侧，且开口向上，可得a＞0， ＞0，所以b＜0，然后由二次函数的图象与y轴交于y轴的负半轴，得c＜0，即可得到a＞0，bc＞0，则点P（a，bc）在第一象限．
故答案为：一． 二次函数y=ax2+bx+c的图象如图所示，给出下列说法：①ac＞0；②2a+b=0；③a+b+c=0；④当x＞1时，函数y随x的增大而增大；⑤当y＞0时，-1＜x＜3．其中，正确的说法有___________（请写出所有正确说法的序号）．
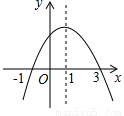
②⑤
【解析】试题解析：：∵抛物线的开口向下，与y轴的交点在y轴的正半轴上，
∴a＜0，c＞0，
∴ac＜0，∴①错误；
由图象可知：-=1，
∴2a+b=0，∴②正确；
当x=1时，y=a+b+c＞0，∴③错误；
由图象可知：当x＞1时，函数y随x的增大而减小，∴④错误；
根据图象，当-1＜x＜3时，y＞0，∴⑤正确；
正确的说法有②⑤． 已知抛物线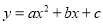
（a＜0）过A（-2，0）、O（0，0）、B（-3， 
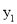）、C（3， 
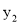）四点，则
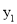与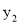
的大小关系是__________
【解析】由已知得抛物线与x轴交于A（-2，0）、O（0，0）两点，开口向下，对称轴为x==-1，可知B（-3， ）、C（3， ）两点在对称轴的两边，点B离对称轴较近，再根据抛物线图象可得．
故答案为： ． 已知抛物线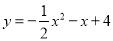
．
（1）用配方法求它的顶点坐标、对称轴；
（2）x取何值时，y随x增大而减小？
（3）x取何值时，抛物线在x轴上方？
（1）顶点坐标为（-1， ），对称轴为：x= -1；（2）x﹥-1时，随增大而减小 ；（3）-4﹤x﹤2时，抛物线在x轴上方．
【解析】试题分析：（1）用配方法时，先提二次项系数，再配方，写成顶点式，根据顶点式的坐标特点求顶点坐标及对称轴；
（2）对称轴是x=-1，开口向下，根据对称轴及开口方向确定函数的增减性；
（3）令y=0，确定函数图象与x轴的交点，结合开口方向判断x的取值... 用配方法把函数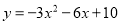
化成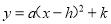
的形式，然后指出它的图象开口方向，对称轴，顶点坐标和最值．
向下，x=-1，（-1，13），最大值13
【解析】试题分析：根据这个函数的二次项系数是-3，配方法变形成的形式，直接可判断出开口方向，对称轴，顶点坐标和最值.
试题解析：∵，
∴开口向下，对称轴x=-1，顶点坐标（-1，13），最大值13． 已知m，n是关于x的方程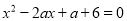
的两实根，求
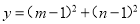的最小值．
8
【解析】试题分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把整理成m+n与mn的形式，代入进行计算求解．
试题解析：依题意△=≥0，
即，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
即
=
=
=，
∴a=3时，y的最小值为8．
故答案为：8． 把抛物线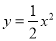
平移得到抛物线m，抛物线m经过点A（-6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线
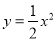交于点Q．
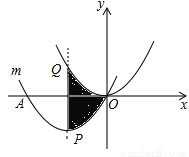
（1）求顶点P的坐标；
（2）写出平移过程；
（3）求图中阴影部分的面积．
（1）（-3， ）；（2）先向左平移3个单位，再向下平移个单位；（3）.
【解析】试题分析：（1）先利用交点式确定平移后的抛物线解析式，然后配成顶点式得到P点坐标；
（2）利用顶点的平移过程得到抛物线的平移过程；
（3）根据平移得到图中阴影部分的面积，然后根据三角形面积公式计算．
试题解析：（1）平移的抛物线解析式为= =，
所以顶点P的坐标为（-3， ）；
（...