题目内容
黄冈中学是百年名校,百年校庆上的焰火晚会令很多人记忆犹新.有一种焰火升高高度为h(m)与飞行时间t(s)的关系式是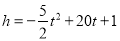 ,若这种焰火在点燃升空后到最高处引爆,则从点火到引爆所需时间为__________s.
,若这种焰火在点燃升空后到最高处引爆,则从点火到引爆所需时间为__________s.
 4
【解析】根据关系式可知焰火的运行轨迹是一个开口向下的抛物线,已知焰火在升到最高时引爆,即到达抛物线的顶点时引爆,顶点横坐标就是从点火到引爆所需时间.则t==4s,
故答案为:4.
4
【解析】根据关系式可知焰火的运行轨迹是一个开口向下的抛物线,已知焰火在升到最高时引爆,即到达抛物线的顶点时引爆,顶点横坐标就是从点火到引爆所需时间.则t==4s,
故答案为:4.
练习册系列答案
相关题目
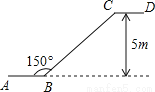
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
A.5cm B.5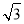 cm C.10m D.
cm C.10m D.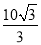 m
m
 C.
【解析】
试题分析:如图所示:过点C作CE⊥AB延长线于点E,
∵∠ABC=150°,
∴∠CBE=30°,
∵从点B到点C上升的高度为5m,
∴电梯BC的长是10m.
故选C.
C.
【解析】
试题分析:如图所示:过点C作CE⊥AB延长线于点E,
∵∠ABC=150°,
∴∠CBE=30°,
∵从点B到点C上升的高度为5m,
∴电梯BC的长是10m.
故选C. 分解因式: 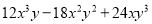 =6xy(______)
=6xy(______)
 【解析】 =6xy().
【解析】 =6xy(). 下列各式从左到右的变形中,是因式分解的是( ).
A. x(a-b)=ax-bx B. x2-1+y2=(x-1)(x+1)+y2
C. y2-1=(y+1)(y-1) D. ax+bx+c=x(a+b)+c
 C
【解析】A. 是整式的乘法,故A错误;
B. 没把一个多项式转化成几个整式积,故B错误;
C. 把一个多项式转化成几个整式积,故C正确;
D. 没把一个多项式转化成几个整式积,故D错误;
故选:C.
C
【解析】A. 是整式的乘法,故A错误;
B. 没把一个多项式转化成几个整式积,故B错误;
C. 把一个多项式转化成几个整式积,故C正确;
D. 没把一个多项式转化成几个整式积,故D错误;
故选:C. 用配方法把函数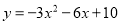 化成
化成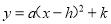 的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.
的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.
 向下,x=-1,(-1,13),最大值13
【解析】试题分析:根据这个函数的二次项系数是-3,配方法变形成的形式,直接可判断出开口方向,对称轴,顶点坐标和最值.
试题解析:∵,
∴开口向下,对称轴x=-1,顶点坐标(-1,13),最大值13.
向下,x=-1,(-1,13),最大值13
【解析】试题分析:根据这个函数的二次项系数是-3,配方法变形成的形式,直接可判断出开口方向,对称轴,顶点坐标和最值.
试题解析:∵,
∴开口向下,对称轴x=-1,顶点坐标(-1,13),最大值13. 若函数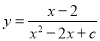 的自变量x的取值范围是全体实数,则c的取值范围是( )
的自变量x的取值范围是全体实数,则c的取值范围是( )
A. c>1
B. c=1
C. c<1
D. c≤1
 A
【解析】先根据分式的意义,分母不等于0,得出,再根据二次函数(a≠0)的图象性质,可知当二次项系数a>0,△=时,有y>0,此时自变量x的取值范围是全体实数,解得c>1.
故选:A.
A
【解析】先根据分式的意义,分母不等于0,得出,再根据二次函数(a≠0)的图象性质,可知当二次项系数a>0,△=时,有y>0,此时自变量x的取值范围是全体实数,解得c>1.
故选:A. 在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( )
A. 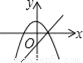 B.
B. 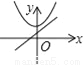 C.
C. 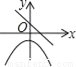 D.
D. 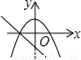
 D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D.
D
【解析】试题分析: A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
故选:D. 已知抛物线的顶点坐标为P(2,-1),它的图象经过点C(0,3).
(1)求该抛物线的解析式.
(2)设该抛物线的图象与x轴交于A、B两点,求△ABC的面积.
 (1);(2)3
【解析】分析:(1)设该抛物线方程为 ,然后将点(3,0)代入求得k的值;(2)令y=0,求出抛物线与x轴的交点坐标,然后根据三角形的面积公式列式计算求解.
本题解析:(1)∵抛物线的顶点坐标为P(2,-1),
∴设该抛物线方程为,(k≠0);
∵它的图象经过点C(0,3),
∴,
解得k=1,
∴该抛物线的解析式为,即;
(2)令...
(1);(2)3
【解析】分析:(1)设该抛物线方程为 ,然后将点(3,0)代入求得k的值;(2)令y=0,求出抛物线与x轴的交点坐标,然后根据三角形的面积公式列式计算求解.
本题解析:(1)∵抛物线的顶点坐标为P(2,-1),
∴设该抛物线方程为,(k≠0);
∵它的图象经过点C(0,3),
∴,
解得k=1,
∴该抛物线的解析式为,即;
(2)令... 分式方程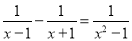 去分母时,两边都乘以________.
去分母时,两边都乘以________.
 (x+1)(x-1))
【解析】∵分式方程 可化为: ,
∴去分母时,方程两边应都乘以: .
(x+1)(x-1))
【解析】∵分式方程 可化为: ,
∴去分母时,方程两边应都乘以: . 
