题目内容
已知抛物线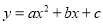 (a<0)过A(-2,0)、O(0,0)、B(-3,
(a<0)过A(-2,0)、O(0,0)、B(-3, 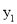 )、C(3,
)、C(3, 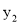 )四点,则
)四点,则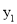 与
与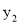 的大小关系是__________
的大小关系是__________
 【解析】由已知得抛物线与x轴交于A(-2,0)、O(0,0)两点,开口向下,对称轴为x==-1,可知B(-3, )、C(3, )两点在对称轴的两边,点B离对称轴较近,再根据抛物线图象可得.
故答案为: .
【解析】由已知得抛物线与x轴交于A(-2,0)、O(0,0)两点,开口向下,对称轴为x==-1,可知B(-3, )、C(3, )两点在对称轴的两边,点B离对称轴较近,再根据抛物线图象可得.
故答案为: .
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
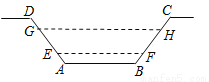
A. 0.55 B. 0.8 C. 0.6 D. 0.75
 D
【解析】试题分析:过点E作EM⊥GH,则GM=(2.1-1.2)÷2=0.45米,根据坡度可得:EM=0.45÷0.6=0.75米,故选D.
D
【解析】试题分析:过点E作EM⊥GH,则GM=(2.1-1.2)÷2=0.45米,根据坡度可得:EM=0.45÷0.6=0.75米,故选D. 把多项式(3a-4b)(7a-8b)+(11a-12b)(8b-7a)分解因式的结果( )
A. 8(7a-8b)(a-b) B. 2(7a-8b)2
C. 8(7a-8b)(b-a) D. -2(7a-8b)
 C
【解析】把(3a-4b)(7a-8b)+(11a-12b)(8b-7a)运用提取公因式法因式分解即可得(3a-4b)(7a-8b)+(11a-12b)(8b-7a)
=(7a-8b)(3a-4b-11a+12b)
=(7a-8b)(-8a+8b)
=8(7a-8b)(b-a).
故选:C.
C
【解析】把(3a-4b)(7a-8b)+(11a-12b)(8b-7a)运用提取公因式法因式分解即可得(3a-4b)(7a-8b)+(11a-12b)(8b-7a)
=(7a-8b)(3a-4b-11a+12b)
=(7a-8b)(-8a+8b)
=8(7a-8b)(b-a).
故选:C. 把多项式(m+1)(m-1)+(m-1)分解因式,一个因式是(m-1),则另一个因式是( )
A. m+1 B. 2m C. 2 D. m+2
 D
【解析】∵(m+1)(m-1)+(m-1)=(m-1)(m+1+1)=(m-1)(m+2),
∴另一个因式是(m+2).
故选D.
D
【解析】∵(m+1)(m-1)+(m-1)=(m-1)(m+1+1)=(m-1)(m+2),
∴另一个因式是(m+2).
故选D. 如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[2,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[4,2],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[2,4]?
 (1)此函数图象的顶点坐标为:(1,0);(2)图象对应的函数的特征数为:[0,﹣1];(3)原函数的图象向右平移1个单位,再向上平移5个单位得到.
【解析】试题分析:(1)根据特征数的定义,得二次函数为y=x2﹣2x+1,再利用配方得:y=(x﹣1)2,从而顶点坐标为(1,0)
(2)①根据特征数的定义,得二次函数为y=x2+2x-1,再利用配方得y=(x+1)2﹣2,图象先向右平移...
(1)此函数图象的顶点坐标为:(1,0);(2)图象对应的函数的特征数为:[0,﹣1];(3)原函数的图象向右平移1个单位,再向上平移5个单位得到.
【解析】试题分析:(1)根据特征数的定义,得二次函数为y=x2﹣2x+1,再利用配方得:y=(x﹣1)2,从而顶点坐标为(1,0)
(2)①根据特征数的定义,得二次函数为y=x2+2x-1,再利用配方得y=(x+1)2﹣2,图象先向右平移... 便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足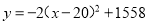 ,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )
,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )
A. 20 B. 1508 C. 1558 D. 1585
 C
【解析】由题意知,一周利润y(元)与每件销售价x(元)之间的关系满足,且15≤x≤22,根据二次函数的开口方向向下,可知当x=20时, .
故选:C.
C
【解析】由题意知,一周利润y(元)与每件销售价x(元)之间的关系满足,且15≤x≤22,根据二次函数的开口方向向下,可知当x=20时, .
故选:C. 已知抛物线y=ax2+bx+c开口向下,顶点坐标(3,-5),那么该抛物线有( )
A. 最小值-5
B. 最大值-5
C. 最小值3
D. 最大值3
 B
【解析】由抛物线的开口向下和其顶点坐标为(3,-5),根据抛物线的性质,可以知该抛物线有最大值-5.
故选:B.
B
【解析】由抛物线的开口向下和其顶点坐标为(3,-5),根据抛物线的性质,可以知该抛物线有最大值-5.
故选:B. 若y=ax2+bx+c,则由表格中信息可知y与x之间的函数表达式是( )
x | -1 | 0 | 1 |
ax2 | 1 | ||
ax2+bx+c | 8 | 3 |
A. y=x2-4x+3 B. y=x2-3x+4
C. y=x2-3x+3 D. y=x2-4x+8
 A
【解析】把表格中所给的的三对对应值代入对应的式子可得: ,解得: ,
∴与之间的函数表达式为:.
故选A.
A
【解析】把表格中所给的的三对对应值代入对应的式子可得: ,解得: ,
∴与之间的函数表达式为:.
故选A. 当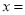 ______时,
______时,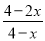 的值与
的值与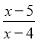 的值相等.
的值相等.
 -1
【解析】本题主要考查了解分式方程. 由题意可得分式方程 =,方程两边同乘以(4-x),去分母,化为整式方程求解.
【解析】
由题意可得分式方程:
=,
方程两边同乘以(4-x),
得4-2x=5-x,
整理得x=-1,
经检验,原方程的解为x=-1.
-1
【解析】本题主要考查了解分式方程. 由题意可得分式方程 =,方程两边同乘以(4-x),去分母,化为整式方程求解.
【解析】
由题意可得分式方程:
=,
方程两边同乘以(4-x),
得4-2x=5-x,
整理得x=-1,
经检验,原方程的解为x=-1. 
