��Ŀ����
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����������˵������ac��0����2a+b=0����a+b+c=0���ܵ�x��1ʱ������y��x����������ݵ�y��0ʱ��-1��x��3�����У���ȷ��˵����___________����д��������ȷ˵������ţ���
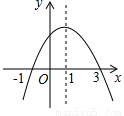
 �ڢ�
��������������������������ߵĿ������£���y��Ľ�����y����������ϣ�
��a��0��c��0��
��ac��0����ٴ���
��ͼ���֪��-=1��
��2a+b=0�������ȷ��
��x=1ʱ��y=a+b+c��0����۴���
��ͼ���֪����x��1ʱ������y��x���������С����ܴ���
����ͼ��-1��x��3ʱ��y��0�������ȷ��
��ȷ��˵���Тڢݣ�
�ڢ�
��������������������������ߵĿ������£���y��Ľ�����y����������ϣ�
��a��0��c��0��
��ac��0����ٴ���
��ͼ���֪��-=1��
��2a+b=0�������ȷ��
��x=1ʱ��y=a+b+c��0����۴���
��ͼ���֪����x��1ʱ������y��x���������С����ܴ���
����ͼ��-1��x��3ʱ��y��0�������ȷ��
��ȷ��˵���Тڢݣ�
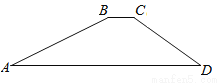
��ͼ��һˮ���ӵĺ����Ϊ����ABCD���Ӷ�BC��6�ף��Ӹ�20�ף�б��AB���¶�i=1��2.5��б��CD���½�Ϊ30�ȣ���ӵ�AD�ij���Ϊ��������
A. 56�� B. 66�� C. ��56+20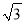 ���� D. ��50
���� D. ��50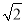 +20
+20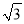 ����
����
 C
�������������������������ɵã�BE=CF=20�ף�����б��AB���±�Ϊ1��2.5�ɵã�AE=50�ף����ݡ�D=30�㣬CF=20�ɵã�DF=�ף���AD=AE+EF+DF=(56+)�ף���ѡC��
C
�������������������������ɵã�BE=CF=20�ף�����б��AB���±�Ϊ1��2.5�ɵã�AE=50�ף����ݡ�D=30�㣬CF=20�ɵã�DF=�ף���AD=AE+EF+DF=(56+)�ף���ѡC�� -6xyz+3xy2-9x2y�Ĺ���ʽ�ǣ� ��
A. -3x B. 3xz C. 3yz D. -3xy
 D
��������ͨ���۲��֪ԭʽ�Ĺ���ʽΪ-3xy��ֱ����ȡ���ɣ�
D
��������ͨ���۲��֪ԭʽ�Ĺ���ʽΪ-3xy��ֱ����ȡ���ɣ� ���и�ʽ����ʽ�ֽ�����ȷ���ǣ� ��
A. -m2+mn-m=-m(m+n-1) B. 9abc-6a2b2=3abc(3-2ab)
C. 3a2x-6bx+3x=3x(a2-2b) D. 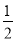 ab2+
ab2+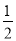 a2b=
a2b=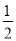 ab(a+b)
ab(a+b)
 D
��������ѡ��A��ԭʽ=-m(m-n+1)��ѡ��B��ԭʽ=3abc(3c-2ab)��ѡ��C��ԭʽ=3x(a2-2b+1)��ѡ��D��ԭʽ=ab(a+b)����ѡD.
D
��������ѡ��A��ԭʽ=-m(m-n+1)��ѡ��B��ԭʽ=3abc(3c-2ab)��ѡ��C��ԭʽ=3x(a2-2b+1)��ѡ��D��ԭʽ=ab(a+b)����ѡD. ��������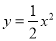 ƽ�Ƶõ�������m��������m������A��-6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������
ƽ�Ƶõ�������m��������m������A��-6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������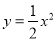 ���ڵ�Q��
���ڵ�Q��
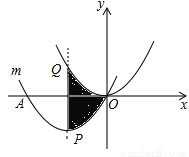
��1����P�����ꣻ
��2��д��ƽ�ƹ��̣�
��3����ͼ����Ӱ���ֵ������
 ��1����-3�� ������2��������ƽ��3����λ��������ƽ�Ƹ���λ����3��.
�������������������1�������ý���ʽȷ��ƽ�ƺ�������߽���ʽ��Ȼ����ɶ���ʽ�õ�P�����ꣻ
��2�����ö����ƽ�ƹ��̵õ������ߵ�ƽ�ƹ��̣�
��3������ƽ�Ƶõ�ͼ����Ӱ���ֵ������Ȼ����������������ʽ���㣮
�����������1��ƽ�Ƶ������߽���ʽΪ= =��
���Զ���P������Ϊ��-3�� ����
��...
��1����-3�� ������2��������ƽ��3����λ��������ƽ�Ƹ���λ����3��.
�������������������1�������ý���ʽȷ��ƽ�ƺ�������߽���ʽ��Ȼ����ɶ���ʽ�õ�P�����ꣻ
��2�����ö����ƽ�ƹ��̵õ������ߵ�ƽ�ƹ��̣�
��3������ƽ�Ƶõ�ͼ����Ӱ���ֵ������Ȼ����������������ʽ���㣮
�����������1��ƽ�Ƶ������߽���ʽΪ= =��
���Զ���P������Ϊ��-3�� ����
��... ֱ������ƽ���Ͻ����κ���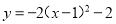 ��ͼ������ƽ��1����λ��������ƽ��1����λ�����䶥��Ϊ��������
��ͼ������ƽ��1����λ��������ƽ��1����λ�����䶥��Ϊ��������
A. ��0��0��
B. ��1��-2��
C. ��0��-1��
D. ��-2��1��
 C
���������������ԭ�����ߵĶ���Ϊ��1��-2����Ȼ����ͼ������ƽ��1����λ��������ƽ��1����λ���ɵ��������ߵĶ���Ϊ��0��-1����
��ѡ��C��
C
���������������ԭ�����ߵĶ���Ϊ��1��-2����Ȼ����ͼ������ƽ��1����λ��������ƽ��1����λ���ɵ��������ߵĶ���Ϊ��0��-1����
��ѡ��C�� ��������ͼ��ʾ������ˮƽֱ��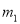 ��
�� 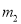 ��
�� 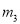 ������һ����Ϊx�ᣨ����Ϊ������������ֱֱ��
������һ����Ϊx�ᣨ����Ϊ������������ֱֱ��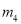 ��
�� 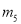 ��
�� 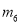 ������һ����Ϊy�ᣨ����Ϊ���������ڴ�����ƽ���ڻ�����������
������һ����Ϊy�ᣨ����Ϊ���������ڴ�����ƽ���ڻ�����������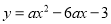 ��������ѡ���x���y��ֱ�Ϊ��������
��������ѡ���x���y��ֱ�Ϊ��������
A. 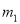 ��
�� 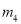
B. 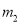 ��
�� 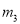
C. 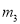 ��
�� 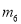
D. 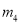 ��
�� 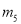
 A
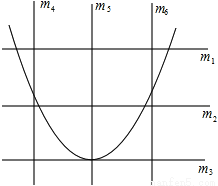
�����������������߿������Ͽ�֪a��0�����������䷽Ϊ���ɵ������ߵĶԳ���Ϊx=3����֪Ӧѡ���y��Ϊֱ�ߣ��ɶ�������Ϊ��3��-3-9a������������y��Ľ���Ϊ��0��-3������-3-9a��-3����֪Ӧѡ���x��Ϊֱ�ߣ�
��ѡ��A��
A
�����������������߿������Ͽ�֪a��0�����������䷽Ϊ���ɵ������ߵĶԳ���Ϊx=3����֪Ӧѡ���y��Ϊֱ�ߣ��ɶ�������Ϊ��3��-3-9a������������y��Ľ���Ϊ��0��-3������-3-9a��-3����֪Ӧѡ���x��Ϊֱ�ߣ�
��ѡ��A�� �������߾�����(3��0)��(2����3)������ֱ��x��1Ϊ�Գ��ᣬ��������ߵĽ���ʽΪ( )
A. y����x2��2x��3 B. y��x2��2x��3
C. y��x2��2x��3 D. y����x2��2x��3
 C
���������������ߵĽ���ʽΪ��y=ax²+bx+c,��(3��0)��(2����3)���������߽���ʽ��: ,
��ֱ��x=1Ϊ�Գ���,�õ�,��b=-2a,
���뷽�����: ,
���:a=1,b=-2,c=-3 ,
�������߽���ʽΪy=x²-2x-3,
����Cѡ������ȷ��
C
���������������ߵĽ���ʽΪ��y=ax²+bx+c,��(3��0)��(2����3)���������߽���ʽ��: ,
��ֱ��x=1Ϊ�Գ���,�õ�,��b=-2a,
���뷽�����: ,
���:a=1,b=-2,c=-3 ,
�������߽���ʽΪy=x²-2x-3,
����Cѡ������ȷ�� ����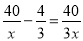 �Ľ���______��
�Ľ���______��
 x=20
����������������ͬʱ��3x����
120-4x=40��
��ã�x=20��
���飺��x=20ʱ��3x=60��0��
����x=20��ԭ���̵ĸ���
�ʴ�Ϊ��x=20.
x=20
����������������ͬʱ��3x����
120-4x=40��
��ã�x=20��
���飺��x=20ʱ��3x=60��0��
����x=20��ԭ���̵ĸ���
�ʴ�Ϊ��x=20. 
