某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润y（元/千度））与电价x（元/千度）的函数图象如图：
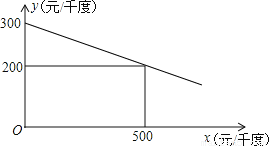
（1）当电价为600元/千度时，工厂消耗每千度电产生利润是多少？
（2）为了实现节能减排目标，有关部门规定，该厂电价x（元/千度）与每天用电量m（千度）的函数关系为x=10m+500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
（1）工厂消耗每千度电产生利润是180元（2）当工厂每天消耗50千度电时，工厂每天消耗电产生利润为5000元
【解析】试题分析：（1）设y=kx+b（k≠0），利用待定系数法求一次函数解析式解答即可；
（2）根据利润=每天的用电量×每千度电产生利润y，然后整理得到W与m的关系式，再根据二次函数的最值问题解答．
【解析】
（1）设工厂每千度电产生利润y（元/千度）与电价x（元/千... 已知：如图，直线y=3x+3与x轴交于C点，与y轴交于A点，B点在x轴上，△OAB是等腰直角三角形．
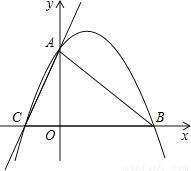
（1）求过A、B、C三点的抛物线的解析式；
（2）若P点是抛物线上的动点，且在第一象限，那么△PAB是否有最大面积？若有，求出此时P点的坐标和△PAB的最大面积；若没有，请说明理由．
（1）y= -x2+2x+3（2）存在,（）
【解析】试题分析：（1）求得直线y=3x+3与坐标轴的两交点坐标，然后根据OB=OA即可求得点B的坐标，然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可；
（2）首先利用待定系数法求得直线AB的解析式，然后根据CD∥AB得到两直线的k值相等，根据直线CD经过点C求得直线CD的解析式，然后求得直线CD和抛物线的交点坐标即可；
... 如图，从热气球C处测得地面A、B两点的俯角分别是30°、45°.如果此时热气球C处的高度CD为100米，点A、D、B在同一直线上，则AB两点的距离是( )
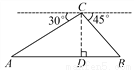
A. 200米 B. 200
米 C. 220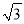
米 D. 100(
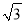＋1)米
D
【解析】试题分析：根据平行线的性质可得：∠A=30°，∠B=45°．在Rt△ACD中，tan∠A=tan30°=，则AD=米；在Rt△CDB中，tan∠B=tan45°=，则AD=100米，故AB=AD+BD=100(+1)米，选D． 如图，小敏同学想测量一棵大树的高度，她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°.已知小敏同学身高(AB)为1.6m，则这棵树的高度为(结果精确到0.1m，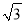 
≈1.73)( )
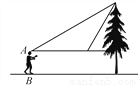
A. 3.5m B. 3.6m C. 4.3m D. 5.1m
D
【解析】如图，设CD＝xm，在Rt△ACD中，∵∠DAC＝30°，∴（m）．在Rt△ECD中，∵∠DEC＝60°，∴（m）．∵AE＝4m，∴，解得．
∴（m）．故选D． 从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（ ）
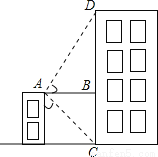
A．（6+6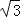
）米 B．（6+3
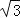）米 C．（6+2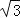）米 D．12米
A
【解析】
试题分析：在Rt△ACB中，∠CAB=45°，AB⊥DC，AB=6，
∴BC=AB=6，
在Rt△ABD中，∵tan∠BAD=，
∴BD=AB•tan∠BAD=6，
∴DC=CB+BD=6+6（m）．
故选A． 如图，为测量一棵与地面垂直的树OA的高度，在距离树的底端30米的B处，测得树顶A的仰角∠ABO为α，则树OA的高度为( )
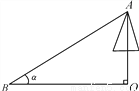
A.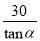 
米 B. 30sinα米 C. 30tanα米 D. 30cosα米
C
【解析】试题解析：在Rt△ABO中，
∵BO=30米，∠ABO为α，
∴AO=BOtanα=30tanα（米）．
故选C． 如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A，C两点测得该塔顶端F的仰角分别为45°和60°，矩形建筑物宽度AD＝20 m，高度DC＝30 m，则信号发射塔顶端到地面的高度(即FG的长)为( )
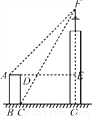
A. (35
＋55)m B. (25
＋45)m C. (25
＋75)m D. (50＋20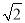
)m
C
【解析】设CG=xm,由图可以知道:EF=(x+20) ·,FG=x·,
则(x+20) ·+30= x·,
计算出x=,
则FG= x·==m,
故选C. 如图，某同学在楼房的A处测得荷塘的一端B处的俯角为30°，荷塘另一端D与点C、B在同一条直线上．已知AC＝32米，CD＝16米，则荷塘宽BD为________米(取
≈1.73，结果保留整数)．
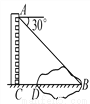
39
【解析】试题分析：根据题意可得：∠B=30°，在Rt△ABC中，tan∠B=tan30°=，则BC=32≈55米，则BD=BC-CD=55-16=39米． 如图，在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°，底部D处的俯角为45°，则这个建筑物的高度CD＝_________米(结果保留根号)．
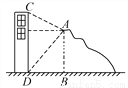
(7＋＋21)
【解析】试题分析：作AE⊥CD于点E．在Rt△ABD中，∠ADB=45°，∴DE=AE=BD=AB=21（米），
在Rt△AEC中，CE=AE•tan∠CAE=21×=7（米）．则CD=（21+7）米． 如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为 m（结果不作近似计算）．
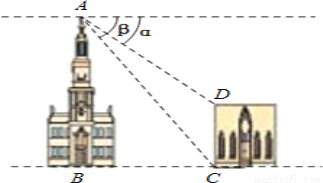
【解析】
试题分析：过点D作DE⊥AB于点E，
则四边形BCDE是矩形，
根据题意得：∠ACB=β=60°，∠ADE=α=30°，BC=18m，
∴DE=BC=18m，CD=BE，
在Rt△ABC中，AB=BC•tan∠ACB=18×tan60°=18（m），
在Rt△ADE中，AE=DE•tan∠ADE=18×tan30°=6（m），
∴DC=BE=AB...