题目内容
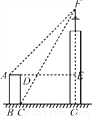
如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A，C两点测得该塔顶端F的仰角分别为45°和60°，矩形建筑物宽度AD＝20 m，高度DC＝30 m，则信号发射塔顶端到地面的高度(即FG的长)为( )
A. (35
＋55)m B. (25
＋45)m C. (25
＋75)m D. (50＋20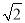
)m
C
【解析】设CG=xm,由图可以知道:EF=(x+20) ·,FG=x·,
则(x+20) ·+30= x·,
计算出x=,
则FG= x·==m,
故选C.
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案如图，已知抛物线与x轴的一个交点A（1，0），对称轴是x= -1，则该抛物线与x轴的另一交点坐标是（ ）
A. （-3，0） B. （-2，0） C. x= -3 D. x= -2
A
【解析】抛物线与x轴的另一交点为B(b，0)，
∵抛物线与x轴的一个交点A(1，0)，对称轴是x＝－1，∴＝－1，
解得b＝－3，∴B(－3，0)． 下列图形中，不一定是轴对称图形的是（ ）
A. 三角形 B. 射线 C. 角 D. 相交的两条直线
A
【解析】题中给出的四个选项中，射线以其所在直线为对称轴，角以其角平分线所在直线为对称轴，相交的两条直线以其夹角的平分线所在直线为对称轴.
故选：A. 如图所示，A，B两地之间有一座山，汽车原来从A地到B地需要经C地沿折线A—C—B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC＝10 km，∠A＝30°，∠B＝45°，则隧道开通后，汽车从A地到B地比原来少走多少千米?(结果精确到0.1 km,参考数据：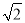 
≈1.41， 
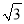≈1.73)
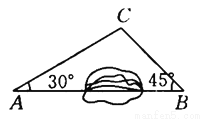
隧道开通后，汽车从A地到B地比原来少走约3.4 km
【解析】试题分析：过点C作AB的垂线CD，垂足为D，在直角△ACD和直角△CBD中，解直角三角形求出CD，AD，BC，就可以得到结论．
试题解析：过点C作AB的垂线CD，垂足为D．
∵AC=10km，∠A=30°，
∴CD=AC=5（km）．
AD==5（km）．
在Rt△CDB中，
∵∠B=45°，
... 如图，小山顶上有一信号塔AB，山坡BC的倾角为30°，现为了测量塔高AB，测量人员选择山脚C处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E处，再测得塔顶仰角为60°，求塔高AB.（结果保留整数
）
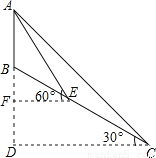
塔高AB大约为58米
【解析】【解析】
依题意可得：∠AEB=30°，∠ACE=15°，
又∵∠AEB=∠ACE+∠CAE，∴∠CAE=15°。
∴△ACE为等腰三角形。∴AE=CE=100米。
在Rt△AEF中，∠AEF=60°，∴EF=AEcos60°=50（米），AF=AEsin60°=50（米）。
在Rt△BEF中，∠BEF=30°，∴BF=EFtan30°... 已知：如图，直线y=3x+3与x轴交于C点，与y轴交于A点，B点在x轴上，△OAB是等腰直角三角形．
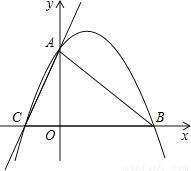
（1）求过A、B、C三点的抛物线的解析式；
（2）若P点是抛物线上的动点，且在第一象限，那么△PAB是否有最大面积？若有，求出此时P点的坐标和△PAB的最大面积；若没有，请说明理由．
（1）y= -x2+2x+3（2）存在,（）
【解析】试题分析：（1）求得直线y=3x+3与坐标轴的两交点坐标，然后根据OB=OA即可求得点B的坐标，然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可；
（2）首先利用待定系数法求得直线AB的解析式，然后根据CD∥AB得到两直线的k值相等，根据直线CD经过点C求得直线CD的解析式，然后求得直线CD和抛物线的交点坐标即可；
... 如图，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米，AC与MN在同一直线上，开始时点A与点N重合，让△ABC以每秒2厘米的速度向左运动，最终点A与点M重合，则重叠部分面积y（厘米2）与时间t（秒）之间的函数关系式为____
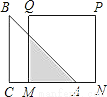
y=（20-2t）2
【解析】AM=20-2t，则重叠部分面积y=×AM2= （20-2t）2 在一幅长60cm，宽40cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是ycm2，设金色纸边的宽度为xcm2，那么y关于x的函数是（ ）
A. y=（60+2x）（40+2x） B. y=（60+x）（40+x）
C. y=（60+2x）（40+x） D. y=（60+x）（40+2x）
A
【解析】长是：60+2x，宽是：40+2x，
由矩形的面积公式得
则y=（60+2x）（40+2x）．
故选A． 某市烟花厂为该市4.18烟花三月经贸旅游特别设计制作一种新型礼炮，这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h＝－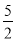
t2＋20t＋1.若这种礼炮点火开空到最高点处引爆，则从点火升空到引爆需要的时间为( )
A. 3s B. 4s C. 5s D. 6s
B
【解析】把二次函数的一般式写成顶点式h=-t2+20t+1=-（t-4）2+41，找出顶点坐标（4，41），当t=4时，升到最高点．
故选：B．