题目内容
如图，从热气球C处测得地面A、B两点的俯角分别是30°、45°.如果此时热气球C处的高度CD为100米，点A、D、B在同一直线上，则AB两点的距离是( )
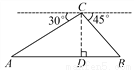
A. 200米 B. 200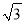
米 C. 220
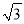米 D. 100(
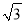＋1)米
D
【解析】试题分析：根据平行线的性质可得：∠A=30°，∠B=45°．在Rt△ACD中，tan∠A=tan30°=，则AD=米；在Rt△CDB中，tan∠B=tan45°=，则AD=100米，故AB=AD+BD=100(+1)米，选D．
利用分解因式计算：
（1）2022+202×196+982
（2）（﹣2）100+（﹣2）100．
（1）90000；（2）2101．
【解析】试题分析：（1）通过观察，显然符合完全平方公式，利用完全平方公式分解因式计算．
（2）利用提取公因式法进行因式分解进行计算．
【解析】
（1）原式=2022+2×202×98+982
=（202+98）2
=3002
=90000．
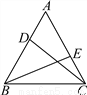
（2）原式=（﹣2）100×（1+1）=2101． 如图，已知在等边三角形ABC中，D、E分别是AB、AC上的点，且AD＝CE.求证：CD＝BE.
见解析
【解析】试题分析：首先根据等边三角形的性质得出∠A=∠BCE=60°，AC=BC，结合已知条件得出△ADC和△CEB全等，从而得出答案．
试题解析：∵△ABC为等边三角形， ∴∠A=∠BCE=60°，AC=BC，
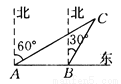
又∵AD=CE， ∴△ADC≌△CEB(SAS)， ∴CD=BE． 如图所示，一艘渔船正以30海里／时的速度由西向东追赶鱼群，自A处经半小时到达B处，在A处看见小岛C在船的北偏东60°的方向上，在B处看见小岛C在船的北偏东30°的方向上，已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区，则这艘船继续向东追赶鱼群，是否有进入危险区域的可能?
不会进入危险区
【解析】试题分析：根据题意实质是比较C点到AB的距离与10的大小．因此作CD⊥AB于D点，求CD的长．
【解析】
作CD⊥AB于D，
根据题意，AB=30×=15，∠CAD=30°，∠CBD=60°，
在Rt△ACD中，AD==CD，
在Rt△BCD中，BD==CD，
∵AB=AD﹣BD，
∴CD﹣CD=15，
CD=＞10，
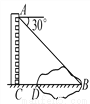
... 如图，某同学在楼房的A处测得荷塘的一端B处的俯角为30°，荷塘另一端D与点C、B在同一条直线上．已知AC＝32米，CD＝16米，则荷塘宽BD为________米(取
≈1.73，结果保留整数)．
39
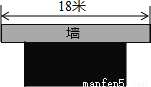
【解析】试题分析：根据题意可得：∠B=30°，在Rt△ABC中，tan∠B=tan30°=，则BC=32≈55米，则BD=BC-CD=55-16=39米． 扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？
当矩形的长为15m，宽为7.5m时，矩形菜园的面积最大，最大面积为112.5m2
【解析】试题分析：设菜园宽为x，则长为36-2x，由面积公式写出y与x的函数关系式，然后利用二次函数的最值的知识可得出菜园的最大面积，及取得最大面积时矩形的长和宽．
设长为x米，宽为(30-x)/2米-,面积为y米2
当x=15时，y最大=112.5
答：最大面积是112.5米2． 如图，某校的围墙由一段相同的凹曲拱组成，其拱状图形为抛物线的一部分，栅栏的跨径AB间，按相同间隔0.2米用5根立柱加固，拱高OC为0.36米，则立柱EF的长为（ ）
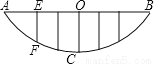
A. 0.4米 B. 0.16米 C. 0.2米 D. 0.24米
C
【解析】如图，以C坐标系的原点，OC所在直线为y轴建立坐标系，
设抛物线解析式为y=ax2，由题知，图象过B（0.6，0.36），代入得：0.36=0.36a
∴a=1，即y=x2．∵F点横坐标为-0.4，∴当x=-0.4时，y=0.16，∴EF=0.36-0.16=0.2米.故选C． 如果一个二次函数的图象经过点A(6，10)，与x轴交于B，C两点，点B，C的横坐标分别为x1，x2，且x1＋x2＝6，x1x2＝5，求这个二次函数的解析式．
解析式为y＝2x2－12x＋10．
【解析】试题分析：设交点式为y=a（x﹣x1）（x﹣x2），再展开合并后把x1+x2=6，x1x2=5代入可得y=a（x2﹣6x+5），然后把A点坐标代入求出a的值即可．
试题解析：【解析】
∵抛物线与x轴交于B，C两点，点B，C的横坐标分别为x1，x2，∴抛物线解析式可设为y=a（x﹣x1）（x﹣x2）=a[x2﹣（x1+x2）x+x1x2]，而... 若二次函数y＝x2＋bx＋4配方后为y＝(x－2)2＋k，则b、k的值分别为( )
A. 0，5 B. 0，1 C. －4，5 D. －4，0
D
【解析】∵二次函数y＝x2＋bx＋4配方后是y＝（x－2）2＋k
∴a=1， -=2， c=4
∴b=-4
∴ k==1
故选：D.