题目内容
已知：如图，直线y=3x+3与x轴交于C点，与y轴交于A点，B点在x轴上，△OAB是等腰直角三角形．
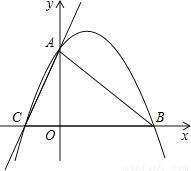
（1）求过A、B、C三点的抛物线的解析式；
（2）若P点是抛物线上的动点，且在第一象限，那么△PAB是否有最大面积？若有，求出此时P点的坐标和△PAB的最大面积；若没有，请说明理由．
（1）y= -x2+2x+3（2）存在,（）
【解析】试题分析：（1）求得直线y=3x+3与坐标轴的两交点坐标，然后根据OB=OA即可求得点B的坐标，然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可；
（2）首先利用待定系数法求得直线AB的解析式，然后根据CD∥AB得到两直线的k值相等，根据直线CD经过点C求得直线CD的解析式，然后求得直线CD和抛物线的交点坐标即可；
...
因式分【解析】
（1）20a3﹣30a2
（2）16﹣（2a+3b）2
（3）﹣16x2y2+12xy3z
（4）5x2y﹣25x2y2+40x3y
（5）x2（a﹣b）2﹣y2（b﹣a）2
（6）（a2+b2）2﹣4a2b2
（7）18b（a﹣b）2+12（b﹣a）3
（8）x（x2+1）2﹣4x3
（9）（x2﹣2x）2﹣3（x2﹣2x）
（10）（2x﹣1）2﹣6（2x﹣1）+9
（11）16x4﹣72x2y2+81y4
（12）a5﹣a
（13）25（x+y）2﹣9（x﹣y）2
（14）m2﹣3m﹣28
（15）x2+x﹣20．
（1）10a2（2a﹣3）；（2）（4+2a+3b）（4﹣2a﹣3b）；
（3）﹣4xy2（4x﹣3yz）；
（4）5x2y（1﹣5y+8x）；
（5）（a﹣b）2（x+y）（x﹣y）；
（6）（a+b）2（a﹣b）2；
（7）6（b﹣a）2（5b﹣2a）；
（8）x（x+1）2（x﹣1）2；
（9）x（x﹣2）（x﹣3）（x+1）；
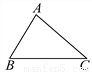
（10）4（x... 如图，在△ABC中，∠B≠∠C.求证：AB≠AC.
见解析
【解析】试题分析：首先假设AB=AC，从而得出与已知条件矛盾，从而得出答案．
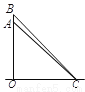
试题解析：假设AB=AC， 则∠B=∠C，∴与已知矛盾，∴AB≠AC． 如图,一枚运载火箭从地面
处发射,当火箭到达
点时,从地面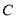
处的雷达站测得
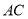的距离是
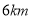,仰角是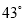
,
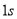后,火箭到达
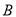点,此时测得
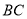的距离是
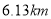,仰角为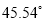
,这枚火箭从
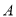点到
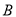点的平均速度是多少?(精确到
)
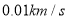这枚火箭从点到点的平均速度是
【解析】试题分析：首先根据Rt△BCO中∠BCO的正弦值得出OB的长度，然后根据Rt△ACO中∠ACO的正弦值得出OA的长度，从而得出答案．
试题解析：在Rt中,
∴
在Rt中, ∴
∴
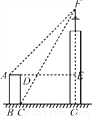
答:这枚火箭从点到点的平均速度是. 如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A，C两点测得该塔顶端F的仰角分别为45°和60°，矩形建筑物宽度AD＝20 m，高度DC＝30 m，则信号发射塔顶端到地面的高度(即FG的长)为( )
A. (35
＋55)m B. (25
＋45)m C. (25
＋75)m D. (50＋20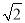
)m
C
【解析】设CG=xm,由图可以知道:EF=(x+20) ·,FG=x·,
则(x+20) ·+30= x·,
计算出x=,
则FG= x·==m,
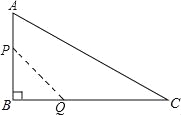
故选C. 如图，在△ABC中，∠B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过 秒，四边形APQC的面积最小．
3
【解析】
试题分析：根据等量关系“四边形APQC的面积=三角形ABC的面积﹣三角形PBQ的面积”列出函数关系
最小值． 设P、Q同时出发后经过的时间为ts，四边形APQC的面积为Smm2，
则有：S=S△ABC﹣S△PBQ==4t2﹣24t+144=4（t﹣3）2+108．
∵4＞0 ∴当t=3s时，S取得最小值． 如图，一边靠校园围墙，其他三边用总长为40米的铁栏杆围成一个矩形花圃，设矩形ABCD的边AB为x米，面积为S平方米，要使矩形ABCD面积最大，则x的长为（ ）
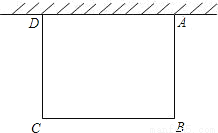
A. 10米 B. 15米 C. 20米 D. 25米
A
【解析】设矩形ABCD的边AB为x米，则宽为40-2x，
S=（40-2x）x= -2x2+40x．
要使矩形ABCD面积最大，
则
即x的长为10m．
故选A． 如图，已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1，0)，B(x2，0) ， 且x1+x2=4， 
.
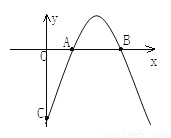
(1)求抛物线的代数表达式;
(2)设抛物线与y轴交于C点，求直线BC的表达式;
(3)求△ABC的面积.
（1）该抛物线的代数表达式为y=-x2+4x-3；（2）直线BC的代数表达式为y=x-3；（3）S△ABC=3.
【解析】试题分析：（1）先解方程组, 求得x1、x2的值，再代入抛物线y=-x2+bx+c即可求得抛物线的代数表达式；
（2）设直线BC的表达式为y=kx+m，先求得抛物线与y轴的交点坐标，再根据待定系数法即可求得直线BC的表达式；
（3）分别求出AB、OC的长，再根... 抛物线y＝2(x－3)2＋1的顶点坐标是( )
A. (3，1) B. (3，－1) C. (－3，1) D. (－3，－1)
A
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y＝2(x－3)2＋1的顶点坐标是（3，1）．
故选：A．