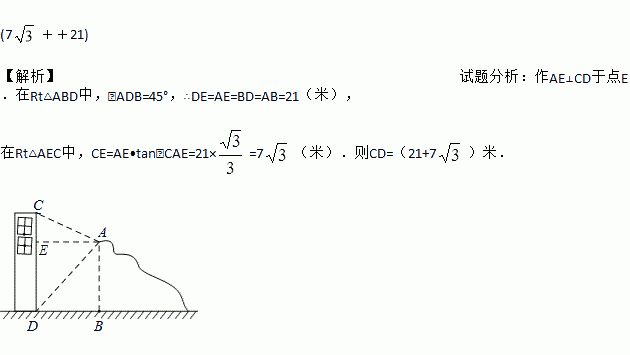题目内容
如图，在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°，底部D处的俯角为45°，则这个建筑物的高度CD＝_________米(结果保留根号)．
(7＋＋21)
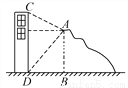
【解析】试题分析：作AE⊥CD于点E．在Rt△ABD中，∠ADB=45°，∴DE=AE=BD=AB=21（米），
在Rt△AEC中，CE=AE•tan∠CAE=21×=7（米）．则CD=（21+7）米．
若x1，x2（x1＜x2）是方程（x-a）（x-b）=1（a＜b）的两个根，则实数x1，x2，a，b的大小关系为（ ）
A. x1＜x2＜a＜b B. x1＜a＜x2＜b
C. x1＜a＜b＜x2 D. a＜x1＜b＜x2
C
【解析】试题分析：用作图法比较简单，首先作出（x﹣a）（x﹣b）=0图象，随便画一个（开口向上的，与x轴有两个交点），再向下平移一个单位，就是（x﹣a）（x﹣b）=1，这时与x轴的交点就是x1，x2，画在同一坐标系下，很容易发现：答案是：x1＜a＜b＜x2．
故选：C． 角、线段、三角形、圆、长方形和正方形中，一定是轴对称图形的有（ ）
A. 4个 B. 5个 C. 6个 D. 3个
B
【解析】通过分析可知，角、线段、圆、长方形和正方形都是轴对称图形，
故选：B. 下列能断定△ABC为等腰三角形的是（ ）
A.∠A=30°，∠B=60° B.∠A=50°，∠B=80°
C.AB=AC=2，BC=4 D.AB=3，BC=7，周长为10
B
【解析】
试题分析：A、B根据三角形的内角和求出第三个角，可得结果；C不能组成三角形，D利用周长求出第三边即可得到答案，根据等腰三角形的判定，采用逐条分析排除的方法判断．
【解析】
A、根据三角形内角和定理得，∠C=180°﹣60°﹣30°=90°，故不是等腰三角形；
B、根据三角形内角和定理得，∠C=180°﹣50°﹣80°=50°，故是等腰三角形；
C、根据... 如图,一枚运载火箭从地面
处发射,当火箭到达
点时,从地面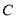
处的雷达站测得
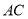的距离是
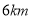,仰角是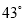
,
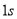后,火箭到达
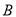点,此时测得
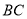的距离是
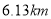,仰角为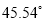
,这枚火箭从
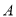点到
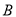点的平均速度是多少?(精确到
)
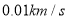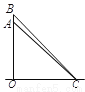
这枚火箭从点到点的平均速度是
【解析】试题分析：首先根据Rt△BCO中∠BCO的正弦值得出OB的长度，然后根据Rt△ACO中∠ACO的正弦值得出OA的长度，从而得出答案．
试题解析：在Rt中,
∴
在Rt中, ∴
∴
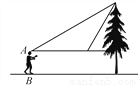
答:这枚火箭从点到点的平均速度是. 如图，小敏同学想测量一棵大树的高度，她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°.已知小敏同学身高(AB)为1.6m，则这棵树的高度为(结果精确到0.1m，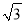 
≈1.73)( )
A. 3.5m B. 3.6m C. 4.3m D. 5.1m
D
【解析】如图，设CD＝xm，在Rt△ACD中，∵∠DAC＝30°，∴（m）．在Rt△ECD中，∵∠DEC＝60°，∴（m）．∵AE＝4m，∴，解得．
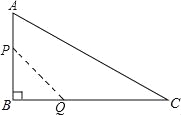
∴（m）．故选D． 如图，在△ABC中，∠B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过 秒，四边形APQC的面积最小．
3
【解析】
试题分析：根据等量关系“四边形APQC的面积=三角形ABC的面积﹣三角形PBQ的面积”列出函数关系
最小值． 设P、Q同时出发后经过的时间为ts，四边形APQC的面积为Smm2，
则有：S=S△ABC﹣S△PBQ==4t2﹣24t+144=4（t﹣3）2+108．
∵4＞0 ∴当t=3s时，S取得最小值． 某公司的生产利润原来是a元，经过连续两年的增长达到了y万元，如果每年增长的百分数都是x，那么y与x的函数关系是（）
A. y=x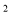
＋a B. y=a（x－1）
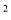C. y=a（1－x）
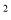D. y=a（1＋x）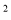
D
【解析】试题分析：根据增长率问题的一般通用公式可得：y=a. 已知二次函数y＝ax2＋bx＋c的图象如图，则下列叙述正确的是( )
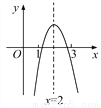
A. abc＜0 B. －3a＋c＜0
C. b2－4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y＝ax2＋c
B
【解析】解：A．由开口向下，可得a＜0；又由抛物线与y轴交于负半轴，可得c＜0，然后由对称轴在y轴右侧，得到b与a异号，则可得b＞0，故得abc＞0，故本选项错误；
B．根据图知对称轴为直线x=2，即=2，得b=﹣4a，再根据图象知当x=1时，y=a+b+c=a﹣4a+c=﹣3a+c＜0，故本选项正确；
C．由抛物线与x轴有两个交点，可得b2﹣4ac＞0，故本选项错误；
...