题目内容
如图，小敏同学想测量一棵大树的高度，她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°.已知小敏同学身高(AB)为1.6m，则这棵树的高度为(结果精确到0.1m，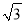 
≈1.73)( )
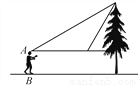
A. 3.5m B. 3.6m C. 4.3m D. 5.1m
D
【解析】如图，设CD＝xm，在Rt△ACD中，∵∠DAC＝30°，∴（m）．在Rt△ECD中，∵∠DEC＝60°，∴（m）．∵AE＝4m，∴，解得．
∴（m）．故选D．
名校课堂系列答案如图，已知二次函数y＝ax2＋bx＋c的部分图象，由图象可知关于x的一元二次方程ax2＋bx＋c＝0的两个根分别是x1＝1.6，x2＝( )
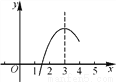
A. －1.6 B. 3.2 C. 4.4 D. 以上都不对
C
【解析】根据图象知道抛物线的对称轴为x=3，根据抛物线是轴对称图象和已知条件即可求出x2．
【解析】
由抛物线图象可知其对称轴为x=3，
又抛物线是轴对称图象，
∴抛物线与x轴的两个交点关于x=3对称，
而关于x的一元二次方程ax2+bx+c=0的两个根分别是x1，x2，
那么两根满足2×3=x1+x2，
而x1=1.6，
∴x2=4.4．
... 等腰三角形是轴对称图形，它的对称轴是( )
A. 过顶点的直线 B. 底边上的高
C. 顶角的平分线所在的直线 D. 腰上的高所在的直线
C
【解析】等腰三角形的对称轴为顶角平分线所在的直线，
故选C． 某地震救援队探测出某建筑物废墟下方点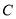
处有生命迹象,已知废墟一侧地面上两探测点A，B相距3米,探测线与地面的夹角分别是
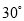和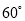
(如图),试确定生命所在点C的深度.(结果精确到
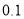米,参考数据: 
,
)
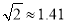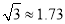生命所在点的深度约为米
【解析】试题分析：过点C作CD⊥AB于点D，根据题意得出∠CAD=30°，∠CBD=60°，分别根据Rt△ACD和Rt△BCD的三角函数将AD和BD用含CD的代数式表示，然后根据AB=3得出答案．
试题解析：过作于点
∵探测线与地面的夹角为和， ∴,，
在Rt中, ， ∴，
在Rt中, ， ∴，
又∵ ∴ 解得，
∴生命所在点的深度... 如图，在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°，底部D处的俯角为45°，则这个建筑物的高度CD＝_________米(结果保留根号)．
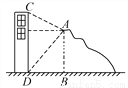
(7＋＋21)
【解析】试题分析：作AE⊥CD于点E．在Rt△ABD中，∠ADB=45°，∴DE=AE=BD=AB=21（米），
在Rt△AEC中，CE=AE•tan∠CAE=21×=7（米）．则CD=（21+7）米． 某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y= -2x+100．（利润=售价-制造成本）
（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
（1）z= -2x2+136x-1800；（2）当销售单价为34元时，每月能获得最大利润，最大利润是512万元；
【解析】试题分析：（1）根据每月的利润z=（x-18）y，再把y=-2x+100代入即可求出z与x之间的函数解析式，
（2）把z=350代入z=-2x2+136x-1800，解这个方程即可，将z═-2x2+136x-1800配方，得z=-2（x-34）2+512，即可求出当... 小敏在某次投篮中，球的运动路线是抛物线y=﹣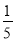
x2+3.5的一部分（如图），若命中篮圈中心，则他与篮底的距离L是（ ）
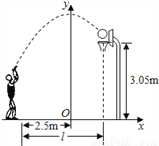
A. 3.5m B. 4m C. 4.5m D. 4.6m
B
【解析】试题分析：如图，把C点纵坐标y=3.05代入y=x2+3.5中得： x=±1.5（舍去负值），
即OB=1.5， 所以L=AB=2.5+1.5=4米，故选B． 已知关于x的方程x2＋(2m＋1)x＋m2＋2＝0有两个不相等的实数根，试判断直线y＝(2m－3)x－4m＋7能否经过点A(－2，4)，并说明理由．
该直线不经过点A，理由见解析.
【解析】试题分析：根据已知求出b2﹣4ac=4m﹣7＞0，确定2m﹣3和﹣4m+7的范围，从而得到图象经过一、三、四象限，即可判断答案．
试题解析：【解析】
该直线不经过点A．理由如下：
∵方程x2＋(2m＋1)x＋m2＋2＝0有两个不相等的实数根，∴△=(2m＋1)2－4(m2＋2)=4m－7＞0，∴2m－＞0，∴2m－3＞0．
又由4m... 抛物线y＝x2＋bx＋c的图象先向右平移2个单位，再向下平移3个单位，所得图象的函数解析式为y＝(x－1)2－4，则b，c的值分别为( )
A. b＝2，c＝－6 B. b＝2，c＝0
C. b＝－6，c＝8 D. b＝－6，c＝2
B
【解析】试题分析：先确定出平移后的抛物线的顶点坐标，然后根据向右平移横坐标加，向下平移纵坐标减求出平移前的抛物线的顶点坐标，然后写出平移前的抛物线的顶点式形式，然后整理成一般形式，即可得到b、c的值．
【解析】
函数y=（x﹣1）2﹣4的顶点坐标为（1，﹣4），
∵是向右平移2个单位，再向下平移3个单位得到，
∴1﹣2=﹣1，﹣4+3=﹣1，
∴平移前的抛物线的...