在△ABC中，AB =AC，∠A=80°，则∠B=__________.
50°
【解析】∵AB=AC，
∴根据轴对称的性质，将线段BC对折重合后，点A在折痕上，
∴线段AB、AC关于折痕轴对称，
设折痕与BC交点为D，
则△ABD、△ACD关于直线AD轴对称，
∴∠B=∠C =(180°－∠A)÷2=（180°－80°)÷2=50°.
故答案为：50°. 已知M、N是线段AB的垂直平分线上任意两点，则∠MAN和∠MBN之间关系是____.
∠MAN=∠MBN
【解析】∵原题当中没有说明点M、N在线段AB的位置，
∴可能有以下四种情况：
①如图①，点M、N在线段AB两侧时，
∵M、N是线段AB的垂直平分线上任意两点，
∴点A、B两点关于直线MN轴对称，
∴线段MA、MB两点关于直线MN轴对称，
同理线段NA、NB两点关于直线MN轴对称，
∴△MAN与△MBN关于直线MN轴对称，
∴... 如图1，在一条河同一岸边有A和B两个村庄，要在河边修建码头M，使M到A和B的距离之和最短，试确定M的位置；
见解析
【解析】试题分析：利用轴对称，作点A关于直线l的对称点A′，连接A′B交直线l于点M，则点M即为所求点.
试题解析：所求点如下图所示：
∵两点之间线段最短，
∴需要能将AM、BM两边转化到一条直线上，
∴用轴对称可以办到，
求点M的位置的具体步骤如下：
①作作点A关于直线BC的轴对称点A’，
②连结A’B交BC于点M，
③连结AM，
... 如图，P和Q为△ABC边AB与AC上两点，在BC边上求作一点M，使△PQM的周长最小．
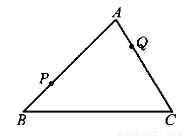
过P点作关于BC对称点P1 连接QP1 交BC于M点
【解析】 圆、长方形、正方形都是轴对称图形，说出他们分别有几条对称轴.
圆、长方形、正方形的对称轴的数量分别是无数条、2条、4条
【解析】试题分析：依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线就是这个轴对称图形的对称轴，据此即可解答．
试题解析：∵对于圆来说，过圆心的任意一条直线，都能够将这个圆分成能够互相重合的两部分
∴过圆心的直线，都是圆的对称轴，
∴圆有无数条... 已知等腰三角形的一边长等于4cm，一边长等于9cm，求它的周长．
22cm
【解析】试题分析：分情况讨论即可；
试题解析：分两种情况：
若腰长为4，4+4<9，不能构成三角形；
若腰长为9，9-9<4，能构成三角形，9+9+4=22，
答：周长是22cm． 如图，长方形ABCD中，AB=2，点E在BC上并且AE=EC，若将矩形纸片沿AE折叠，使点B恰好落在AC上，则AC的长为多少？
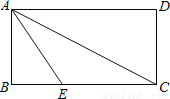
4
【解析】试题分析：根据折叠的性质及等边对等角的性质，可得到∠BAE=∠EAC=∠ECA，根据三角形内角和定理即可求得∠ECA的度数，再根据直角三角形的性质不难求得AC的长．
试题解析：如图，设点B落在AC上后，为点F.
则有△AFE≌△ABE，
∴∠AFE =∠B =90° ，AF =AB =2，
∴FE⊥AC，
∵AE=EC，
∴CF =AF =2，... 下列各式从左到右的变形中，是因式分解的是（ ）.
A. x（a-b）=ax-bx B. x2-1+y2=（x-1）（x+1）+y2
C. y2-1=（y+1）（y-1） D. ax+bx+c=x（a+b）+c
C
【解析】A. 是整式的乘法，故A错误；
B. 没把一个多项式转化成几个整式积，故B错误；
C. 把一个多项式转化成几个整式积，故C正确；
D. 没把一个多项式转化成几个整式积，故D错误；
故选：C. 将多项式-6a3b2-3a2b2+12a2b3分解因式时，应提取的公因式是（ ）
A．-3a2b2 B．-3ab C．-3a2b D．-3a3b3
A
【解析】
在找公因式时，一找系数的最大公约数，二找相同字母的最低次幂．同时注意首项系数通常要变成正数． 下列各式是完全平方式的是（ ）
A. x2+2x﹣1 B. 1+x2 C. x2+xy+1 D. x2﹣x+0.25
D
【解析】A. x2+2x﹣1两个平方项的符号不一致，不是完全平方式；
B. 1+x2缺少两倍的项，不是完全平方式；
C. x2+xy+1缺少两倍的项，不是完全平方式；
D. x2﹣x+0.25=(x-0.5)2,是完全平方式；
故选D.