题目内容
如图1，在一条河同一岸边有A和B两个村庄，要在河边修建码头M，使M到A和B的距离之和最短，试确定M的位置；
见解析
【解析】试题分析：利用轴对称，作点A关于直线l的对称点A′，连接A′B交直线l于点M，则点M即为所求点.
试题解析：所求点如下图所示：
∵两点之间线段最短，
∴需要能将AM、BM两边转化到一条直线上，
∴用轴对称可以办到，
求点M的位置的具体步骤如下：
①作作点A关于直线BC的轴对称点A’，
②连结A’B交BC于点M，
③连结AM，
...
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知点A（﹣1，﹣2），点B（1，4）
（1）试建立相应的平面直角坐标系；
（2）描出线段AB的中点C，并写出其坐标；
（3）将线段AB沿水平方向向右平移3个单位长度得到线段A1B1，写出线段A1B1两个端点及线段中点C1的坐标．
（1）见解析；（2）C（0，1）；（3）平移规律是（x+3，y），所以A1（2，﹣2），B1（4，4），C1（3，1）．
【解析】试题分析：画出平面直角坐标系后描出线段AB的中点C，根据平移的规律求出线段A1B1两个端点及线段中点C1的坐标为A1（2，﹣2），B1（4，4），C1（3，1）．
试题解析：【解析】
（1）坐标系如图：
（2）C（0，1）；
（3）平移规律是（... 二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）
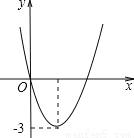
A. -3 B. 3 C. -6 D. 9
B
【解析】先根据抛物线的开口向上可知a＞0，由顶点纵坐标为-3得出b与a关系，再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式，求出m的取值范围即可．
【解析】
∵抛物线的开口向上，顶点纵坐标为-3，
∴a＞0， =-3，即b2=12a，
∵一元二次方程ax2+bx+m=0有实数根，
∴△=b2-4am≥0，即12a-4am≥0，即12-4m≥0，解得m≤3... 5x2﹣25x2y的公因式为__．
5x2
【解析】∵5x2﹣25x2y=5x2(1-y),
∴5x2﹣25x2y的公因式为5x2. 下列各式从左到右的变形中，是因式分解的是（ ）.
A. x（a-b）=ax-bx B. x2-1+y2=（x-1）（x+1）+y2
C. y2-1=（y+1）（y-1） D. ax+bx+c=x（a+b）+c
C
【解析】A. 是整式的乘法，故A错误；
B. 没把一个多项式转化成几个整式积，故B错误；
C. 把一个多项式转化成几个整式积，故C正确；
D. 没把一个多项式转化成几个整式积，故D错误；
故选：C. 等腰三角形的对称轴是______．
顶角平分线所在直线
【解析】一个图形沿一条直线对折，直线两旁的部分能够完全重合，那么这个图形就是轴对称图形，这条直线就是这个图形的一条对称轴,如图所示：等腰三角形的对称轴是顶角平分线所在直线.
故答案是：顶角平分线所在直线. 下列图形中，不是轴对称图形的是（ ）
A. 有两个内角相等的三角形 B. 有一个内角为45°的直角三角形
C. 有两个内角分别为50°和80°的三角形 D. 有两个内角分别为55°和65°的三角形
D
【解析】A.有两个内角相等的三角形是等腰三角形，等腰三角形是轴对称图形；
B.有一个内角为45度的直角三角形是等腰直角三角形，也是等腰三角形，是轴对称图形；C.有两个内角分别为50度和80度的三角形，第三个角是50度，故是等腰三角形，是轴对称图形；
D.有两个内角分别为55度和65度的三角形,不是等腰三角形，不是轴对称图形.
故选：D. 如图，在△ABC中，∠B≠∠C，求证：AB≠AC.当用反证法证明时，第一步应假设( )
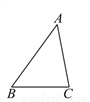
A. ∠B＝∠C B. AB＝AC C. AB＝BC D. ∠A＝∠B
B
【解析】试题分析：利用假设法来进行证明时，首先假设结论成立，即AB=AC，故选B． 如图，从地面竖直向上抛出一个小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的关系式为h=30t-5t2，那么小球从抛出至回落到地面所需要的时间是（ ）
A. 6s B. 4s C. 3s D. 2s
A
【解析】试题分析：由小球高度h与运动时间t的关系式h=30t﹣5t2，令h=0，解得的两值之差便是所要求得的结果．
由小球高度h与运动时间t的关系式h=30t﹣5t2． 令h=0，﹣5t2+30t=0 解得：t1=0，t2=6
△t=6，小球从抛出至回落到地面所需要的时间是6秒．