题目内容
将多项式-6a3b2-3a2b2+12a2b3分解因式时，应提取的公因式是（ ）
A．-3a2b2 B．-3ab C．-3a2b D．-3a3b3
A
【解析】
在找公因式时，一找系数的最大公约数，二找相同字母的最低次幂．同时注意首项系数通常要变成正数．
练习册系列答案
快捷英语周周练系列答案
相关题目
不论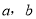
为何有理数, 
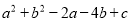的值总是非负数,则c的最小值是( )
A. 4 B. 5 C. 6 D. 无法确定
B
【解析】试题解析：∵a2+b2-2a-4b+c=（a-1）2-1+（b-2）2-4+c=（a-1）2+（b-2）2+c-5≥0，
∴c的最小值是5；
故选B． 已知函数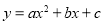
的图象如图所示，那么关于x的方程
的根的情况是（ ）
A．无实数根
B．有两个相等实数根
C．有两个异号实数
D．有两个同号不等实数根
D．
【解析】
试题分析：∵的图象与x轴有两个交点，顶点坐标的纵坐标是﹣3，∵方程，∴时，即是y=﹣2求x的值，由图象可知：有两个同号不等实数根．故选D． 如图所示，根据图形把多项式a2+5ab+4b2因式分解=__．
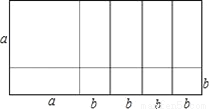
（a+b）（a+4b）
【解析】由图可知，
a2+5ab+4b2=（a+b）（a+4b）. 下面的多项式中，能因式分解的是（ ）
A. m2+n B. m2﹣m+1 C. m2﹣n D. m2﹣2m+1
D
【解析】A. m2+n不能因式分解；
B. m2﹣m+1不能因式分解；
C. m2﹣n不能因式分解；
D. m2﹣2m+1=(m-1)2,能因式分解.
故选D. 如图，P和Q为△ABC边AB与AC上两点，在BC边上求作一点M，使△PQM的周长最小．
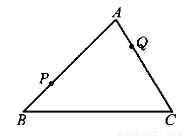
过P点作关于BC对称点P1 连接QP1 交BC于M点
【解析】 等腰三角形有一个是50°，它的一条腰上的高与底边的夹角是（ ）
A. 25° B. 40° C. 25°或40° D. 50°
C
【解析】∵等腰三角形有一个是50°
∴有两种可能
①是三个角为50°、50°、80°；②是三个角为50°、65°、65°分情况说明如下：
①当三个角为50°、50°、80°时，根据图①，可得其一条腰上的高与底边的夹角∠DAB=40°；
②当三个角为50°、65°、65°，根据图②，可得其一条腰上的高与底边的夹角∠DAB=25°故故选：C
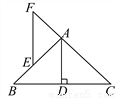
① ② 如图，在△ABC中，AB＝AC，AD⊥BC于D，E是AB上的一点，EF∥AD交CA的延长线于F.
求证：△AEF是等腰三角形．
见解析
【解析】试题分析：首先根据等腰三角形底边上的三线合一定理可得：AD为∠BAC的角平分线，根据平行线的性质得出∠F=∠CAD，∠FEA=∠BAD，从而∠FEA=∠F，得出等腰三角形．
试题解析：∵AB=AC，AD⊥BC， ∴∠BAD=∠CAD， 又∵AD∥EF，
∴∠F=∠CAD，∠FEA=∠BAD， ∴∠FEA=∠F， ∴△AEF是等腰三角形． 如图，隧道的截面是抛物线，可以用y=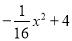 
表示，该隧道内设双行道，限高为3m，那么每条行道宽是（ ）
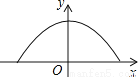
A. 不大于4m B. 恰好4m C. 不小于4m D. 大于4m，小于8m
A
【解析】把y=3代入y= 中得：
x=4，x= -4（舍去）．
∴每条行道宽应不大于4m．
故选A．
点睛；本题考查二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．由题意可知，直接把y=3代入解析式求解即可．