题目内容
在△ABC中，AB =AC，∠A=80°，则∠B=__________.
50°
【解析】∵AB=AC，
∴根据轴对称的性质，将线段BC对折重合后，点A在折痕上，
∴线段AB、AC关于折痕轴对称，
设折痕与BC交点为D，
则△ABD、△ACD关于直线AD轴对称，
∴∠B=∠C =(180°－∠A)÷2=（180°－80°)÷2=50°.
故答案为：50°.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，A、B两点的坐标分别为(2,3)、(4,1)．
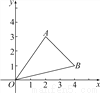
(1)求△ABO的面积；
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
（1）S△ABO＝5；（2）A′(2,0)，B′(4，－2)，O′(0，－3)．
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO＝3×4－×3×2－×4×1－×2×2＝5,
(2)A′(2,0),B′(4,－2),O′(0,－3)． 已知抛物线y＝ax2－2x＋1与x轴没有交点，那么该抛物线的顶点所在的象限是( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
D
【解析】∵抛物线y＝ax2－2x＋1与x轴没有交点，
∴△=4-4a＜0，
解得a＞1，
∴抛物线的开口向上，
又∵b=-2，
∴ ＞0，
∴抛物线的对称轴在y轴的右侧，
∴抛物线的顶点在第一象限.
故选D． 多项式①2x2﹣x，②（x﹣1）2﹣4（x﹣1）+4，③（x+1）2﹣4x（x+1）+4，④﹣4x2﹣1+4x；分解因式后，结果含有相同因式的是（ ）
A. ①④ B. ①② C. ③④ D. ②③
A
【解析】∵①2x2﹣x=x(2x-1)，②（x﹣1）2﹣4（x﹣1）+4=(x﹣3)2，③（x+1）2﹣4x（x+1）+4不能因式分解，④﹣4x2﹣1+4x=-(2x-1)2；
∴①和③含有相同的因式(2x-1).
故选A. 已知等腰三角形的一边长等于4cm，一边长等于9cm，求它的周长．
22cm
【解析】试题分析：分情况讨论即可；
试题解析：分两种情况：
若腰长为4，4+4<9，不能构成三角形；
若腰长为9，9-9<4，能构成三角形，9+9+4=22，
答：周长是22cm． △ABC中，AB=AC，∠A=36°，∠ABC和∠ACB的平分线BE、CD交于点F，则共有等腰三角形( ）
A. 7个 B. 8个 C. 9个 D. 10个
B
【解析】∵等腰三角形有两个角相等，
∴只要能判断出有两个角相等就行了，
将原图各角标上后显示如左下：
因此，所有三角形都是等腰三角形，
只要判断出有哪几个三角形就可以了.
如右上图，三角形有如下几个：
①，②，③；①+②，③+②，①+④，③+④；①+②+③+④；共计8个.
故选：B. 等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中，一定是轴对称图形的有（ ）
A. 3个 B. 4个 C. 5个 D. 2个
A
【解析】等腰三角形、等边三角形、等腰直角三角形都是轴对称图形，是轴对称图形的有3个.
故选：A. 如图所示，已知OC平分∠AOB，CD∥OB，若OD＝3cm，则CD等于( )
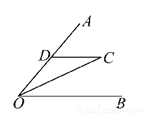
A. 3cm B. 4cm C. 1.5cm D. 2cm
A
【解析】试题分析：根据角平分线的性质可得：∠DOC=∠COB，根据平行线的性质可得：∠DCO=∠COB，则∠DOC=∠DCO，则CD=OD=3cm，故选A． 如图所示是二次函数y=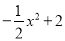
的图象在x轴上方的一部分，对于这段图象与x轴所围成的阴影部分的面积，你认为可能的值是（ ）
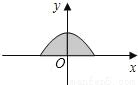
A. 4 B.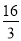 
C. 2π D. 8
B
【解析】函数与y轴交于（0，2）点，与x轴交于（-2，0）和（2，0）两点，则三点构成的三角形面积S1=4，则以半径为2的半圆的面积为S2=π××22=2π，则阴影部分的面积S有：4＜S＜2π．因为选项A、C、D均不在S取值范围内．故选 B