题目内容
已知等腰三角形的一边长等于4cm,一边长等于9cm,求它的周长.
 22cm
【解析】试题分析:分情况讨论即可;
试题解析:分两种情况:
若腰长为4,4+4<9,不能构成三角形;
若腰长为9,9-9<4,能构成三角形,9+9+4=22,
答:周长是22cm.
22cm
【解析】试题分析:分情况讨论即可;
试题解析:分两种情况:
若腰长为4,4+4<9,不能构成三角形;
若腰长为9,9-9<4,能构成三角形,9+9+4=22,
答:周长是22cm.
练习册系列答案
相关题目
一个多项式分解因式的结果是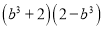 ,那么这个多项式是( )
,那么这个多项式是( )
A. 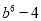 B.
B. 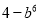 C.
C. 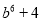 D.
D. 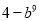
 B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B.
B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B. 已知抛物线y=x2-x-1与x轴的交点为(m,0),则代数式m2-m+2011的值为( )
A. 2009 B. 2012 C. 2011 D. 2010
 B
【解析】∵物线y=x2-x-1与x轴的交点为(m,0),
∴将x=m,y=0代入抛物线解析式得:m2-m-1=0,
∴m2-m=1,
则m2-m+2011=1+2011=2012.
故选:B.
B
【解析】∵物线y=x2-x-1与x轴的交点为(m,0),
∴将x=m,y=0代入抛物线解析式得:m2-m-1=0,
∴m2-m=1,
则m2-m+2011=1+2011=2012.
故选:B. 简便计算:7.292﹣2.712=__.
 45.8
【解析】7.292﹣2.712=(7.29+2.71)(7.29-2.71)=10×4.58=45.8.
45.8
【解析】7.292﹣2.712=(7.29+2.71)(7.29-2.71)=10×4.58=45.8. 下列多项式中能用平方差公式分解因式的是( )
A.a2+(﹣b)2 B.5m2﹣20mn C.﹣x2﹣y2 D.﹣x2+9
 D.
【解析】
试题分析:A、a2+(﹣b)2符号相同,不能用平方差公式分解因式,故A选项错误;
B、5m2﹣20mn两项不都是平方项,不能用平方差公式分解因式,故B选项错误;
C、﹣x2﹣y2符号相同,不能用平方差公式分解因式,故C选项错误;
D、﹣x2+9=﹣x2+32,两项符号相反,能用平方差公式分解因式,故D选项正确.
故选D.
D.
【解析】
试题分析:A、a2+(﹣b)2符号相同,不能用平方差公式分解因式,故A选项错误;
B、5m2﹣20mn两项不都是平方项,不能用平方差公式分解因式,故B选项错误;
C、﹣x2﹣y2符号相同,不能用平方差公式分解因式,故C选项错误;
D、﹣x2+9=﹣x2+32,两项符号相反,能用平方差公式分解因式,故D选项正确.
故选D. 在△ABC中,AB =AC,∠A=80°,则∠B=__________.
 50°
【解析】∵AB=AC,
∴根据轴对称的性质,将线段BC对折重合后,点A在折痕上,
∴线段AB、AC关于折痕轴对称,
设折痕与BC交点为D,
则△ABD、△ACD关于直线AD轴对称,
∴∠B=∠C =(180°-∠A)÷2=(180°-80°)÷2=50°.
故答案为:50°.
50°
【解析】∵AB=AC,
∴根据轴对称的性质,将线段BC对折重合后,点A在折痕上,
∴线段AB、AC关于折痕轴对称,
设折痕与BC交点为D,
则△ABD、△ACD关于直线AD轴对称,
∴∠B=∠C =(180°-∠A)÷2=(180°-80°)÷2=50°.
故答案为:50°. △ABC中,AB =AC,点D在AC上,且BD =BC =AD,则∠A等于( )
A. 30° B. 45° C. 36° D. 72°
 C
【解析】∵有很多等腰三角形,
∴得到很多对称的图形,
∴根据题意将上图构造出来后如下图所示:
∴∠A=36°
故选:C
C
【解析】∵有很多等腰三角形,
∴得到很多对称的图形,
∴根据题意将上图构造出来后如下图所示:
∴∠A=36°
故选:C 用反证法证明命题“对顶角相等”第一步假设__________________.
 对顶角不相等
【解析】试题分析:利用反证法来进行证明时,首先假设结论不成立,即先假设“对顶角不相等”.
对顶角不相等
【解析】试题分析:利用反证法来进行证明时,首先假设结论不成立,即先假设“对顶角不相等”. 将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品的零售价每降价1元,其日销量就增加1个,为了获取每日最大利润,则应降价( )
A. 5元 B. 10元 C. 15元 D. 20元
 A
【解析】设应降价x元,总利润为y元,根据题意可得:
,
化简、配方得:
,
∴当时,y最大=625,
∴ B、C、D错误,选A.
A
【解析】设应降价x元,总利润为y元,根据题意可得:
,
化简、配方得:
,
∴当时,y最大=625,
∴ B、C、D错误,选A. 
