如图所示，根据图形把多项式a2+5ab+4b2因式分解=__．
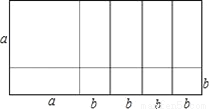
（a+b）（a+4b）
【解析】由图可知，
a2+5ab+4b2=（a+b）（a+4b）. 因式分【解析】
（1）20a3﹣30a2
（2）16﹣（2a+3b）2
（3）﹣16x2y2+12xy3z
（4）5x2y﹣25x2y2+40x3y
（5）x2（a﹣b）2﹣y2（b﹣a）2
（6）（a2+b2）2﹣4a2b2
（7）18b（a﹣b）2+12（b﹣a）3
（8）x（x2+1）2﹣4x3
（9）（x2﹣2x）2﹣3（x2﹣2x）
（10）（2x﹣1）2﹣6（2x﹣1）+9
（11）16x4﹣72x2y2+81y4
（12）a5﹣a
（13）25（x+y）2﹣9（x﹣y）2
（14）m2﹣3m﹣28
（15）x2+x﹣20．
（1）10a2（2a﹣3）；（2）（4+2a+3b）（4﹣2a﹣3b）；
（3）﹣4xy2（4x﹣3yz）；
（4）5x2y（1﹣5y+8x）；
（5）（a﹣b）2（x+y）（x﹣y）；
（6）（a+b）2（a﹣b）2；
（7）6（b﹣a）2（5b﹣2a）；
（8）x（x+1）2（x﹣1）2；
（9）x（x﹣2）（x﹣3）（x+1）；
（10）4（x... 利用分解因式计算：
（1）2022+202×196+982
（2）（﹣2）100+（﹣2）100．
（1）90000；（2）2101．
【解析】试题分析：（1）通过观察，显然符合完全平方公式，利用完全平方公式分解因式计算．
（2）利用提取公因式法进行因式分解进行计算．
【解析】
（1）原式=2022+2×202×98+982
=（202+98）2
=3002
=90000．
（2）原式=（﹣2）100×（1+1）=2101． 如图，已知二次函数y＝ax2＋bx＋c的部分图象，由图象可知关于x的一元二次方程ax2＋bx＋c＝0的两个根分别是x1＝1.6，x2＝( )
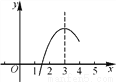
A. －1.6 B. 3.2 C. 4.4 D. 以上都不对
C
【解析】根据图象知道抛物线的对称轴为x=3，根据抛物线是轴对称图象和已知条件即可求出x2．
【解析】
由抛物线图象可知其对称轴为x=3，
又抛物线是轴对称图象，
∴抛物线与x轴的两个交点关于x=3对称，
而关于x的一元二次方程ax2+bx+c=0的两个根分别是x1，x2，
那么两根满足2×3=x1+x2，
而x1=1.6，
∴x2=4.4．
... 如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
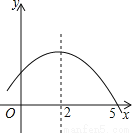
A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5
D
【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0），
∴函数图象与x轴的另一交点坐标为（-1，0），
∴ax2+bx+c＜0的解集是x＜-1或x＞5．
故选C. 二次函数y= -x2+2x+k的部分图象如图所示，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=（ ）
A. 1 B. -1 C. -2 D. 0
B
【解析】试题分析：先把x1=3代入关于x的一元二次方程﹣x2+2x+k=0，求出k的值，再根据根与系数的关系即可求出另一个解x2的值．
【解析】
∵把x1=3代入关于x的一元二次方程﹣x2+2x+k=0得，
﹣9+6+k=0，解得k=3，
∴原方程可化为：﹣x2+2x+3=0，
∴x1+x2=3+x2=﹣=2，解得x2=﹣1．
故选B． 如图，已知抛物线与x轴的一个交点A（1，0），对称轴是x= -1，则该抛物线与x轴的另一交点坐标是（ ）
A. （-3，0） B. （-2，0） C. x= -3 D. x= -2
A
【解析】抛物线与x轴的另一交点为B(b，0)，
∵抛物线与x轴的一个交点A(1，0)，对称轴是x＝－1，∴＝－1，
解得b＝－3，∴B(－3，0)． 抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），这条抛物线的对称轴是（ ）
A. 直线x=1 B. 直线x= -1 C. 直线x=2 D. 直线x= -2
A
【解析】∵抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），
∴这条抛物线的对称轴是：x=，即x=1；
故选：A． 若x1，x2（x1＜x2）是方程（x-a）（x-b）=1（a＜b）的两个根，则实数x1，x2，a，b的大小关系为（ ）
A. x1＜x2＜a＜b B. x1＜a＜x2＜b
C. x1＜a＜b＜x2 D. a＜x1＜b＜x2
C
【解析】试题分析：用作图法比较简单，首先作出（x﹣a）（x﹣b）=0图象，随便画一个（开口向上的，与x轴有两个交点），再向下平移一个单位，就是（x﹣a）（x﹣b）=1，这时与x轴的交点就是x1，x2，画在同一坐标系下，很容易发现：答案是：x1＜a＜b＜x2．
故选：C． 已知抛物线y＝ax2－2x＋1与x轴没有交点，那么该抛物线的顶点所在的象限是( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
D
【解析】∵抛物线y＝ax2－2x＋1与x轴没有交点，
∴△=4-4a＜0，
解得a＞1，
∴抛物线的开口向上，
又∵b=-2，
∴ ＞0，
∴抛物线的对称轴在y轴的右侧，
∴抛物线的顶点在第一象限.
故选D．