题目内容
如图所示，根据图形把多项式a2+5ab+4b2因式分解=__．
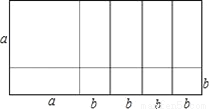
（a+b）（a+4b）
【解析】由图可知，
a2+5ab+4b2=（a+b）（a+4b）.
练习册系列答案
相关题目
分解因式：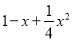 
=____________________.
【解析】1-x+x2=-x+1=( -1)2，
故答案为： . 如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（ ）
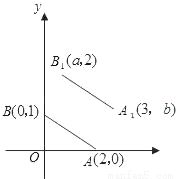
A. 2 B. 3 C. 4 D. 5
A
【解析】由B点平移前后的纵坐标分别为1,2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2,3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2,故选:A. 如图，将二次函数y=31x2-999x+892的图形画在坐标平面上，判断方程31x2-999x+892=0的两根，下列叙述何者正确（ ）
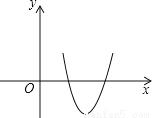
A. 两根相异，且均为正根
B. 两根相异，且只有一个正根
C. 两根相同，且为正根
D. 两根相同，且为负根
A
【解析】∵二次函数y=31x2-999x+892的图象与x轴有两个交点，且与x轴的正半轴相交，
∴方程31x2-999x+892=0有两个正实根．
故选：A． 二次函数y= -x2+2x+k的部分图象如图所示，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=（ ）
A. 1 B. -1 C. -2 D. 0
B
【解析】试题分析：先把x1=3代入关于x的一元二次方程﹣x2+2x+k=0，求出k的值，再根据根与系数的关系即可求出另一个解x2的值．
【解析】
∵把x1=3代入关于x的一元二次方程﹣x2+2x+k=0得，
﹣9+6+k=0，解得k=3，
∴原方程可化为：﹣x2+2x+3=0，
∴x1+x2=3+x2=﹣=2，解得x2=﹣1．
故选B． a2﹣2ab+b2、a2﹣b2的公因式是__．
a﹣b
【解析】∵a2﹣2ab+b2=(a-b)2、a2﹣b2=(a+b)(a-b),
∴a2﹣2ab+b2、a2﹣b2的公因式是a-b. 将多项式-6a3b2-3a2b2+12a2b3分解因式时，应提取的公因式是（ ）
A．-3a2b2 B．-3ab C．-3a2b D．-3a3b3
A
【解析】
在找公因式时，一找系数的最大公约数，二找相同字母的最低次幂．同时注意首项系数通常要变成正数． 有两条或两条以上对称轴的轴对称图形是（ ）
A. 等腰三角形 B. 角 C. 等边三角形 D. 锐角三角形
C
【解析】A.等腰三角形只有一条对称轴；
B.角也只有一条对称轴，是角平分线所在的直线；
C.等边三角形有三条对称轴；
D.锐角三角形的对称轴数量不确定.
故选：C 某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润y（元/千度））与电价x（元/千度）的函数图象如图：
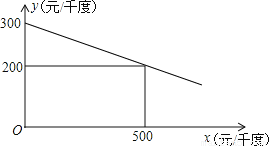
（1）当电价为600元/千度时，工厂消耗每千度电产生利润是多少？
（2）为了实现节能减排目标，有关部门规定，该厂电价x（元/千度）与每天用电量m（千度）的函数关系为x=10m+500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
（1）工厂消耗每千度电产生利润是180元（2）当工厂每天消耗50千度电时，工厂每天消耗电产生利润为5000元
【解析】试题分析：（1）设y=kx+b（k≠0），利用待定系数法求一次函数解析式解答即可；
（2）根据利润=每天的用电量×每千度电产生利润y，然后整理得到W与m的关系式，再根据二次函数的最值问题解答．
【解析】
（1）设工厂每千度电产生利润y（元/千度）与电价x（元/千...