题目内容
如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x= -1,则该抛物线与x轴的另一交点坐标是( )

A. (-3,0) B. (-2,0) C. x= -3 D. x= -2
 A
【解析】抛物线与x轴的另一交点为B(b,0),
∵抛物线与x轴的一个交点A(1,0),对称轴是x=-1,∴=-1,
解得b=-3,∴B(-3,0).
A
【解析】抛物线与x轴的另一交点为B(b,0),
∵抛物线与x轴的一个交点A(1,0),对称轴是x=-1,∴=-1,
解得b=-3,∴B(-3,0).
分解因式:
(1)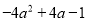 (2)
(2) 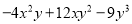
(3)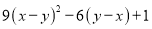 (4)
(4) 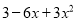
(5)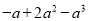 (6)
(6) 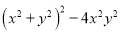
(7)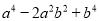 8)
8)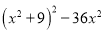
(9)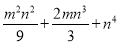 (10)
(10)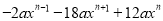
 (1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
...
(1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
... 将四边形ABCD平移后得到四边形A′B′C′D′,已知点A(-1,2)的对应点为A′(-7,10).若将四边形A′B′C′D′看成由四边形ABCD沿A到A′的方向一次平移得到的,则平移的距离为____.
 10
【解析】因为平移后点A(-1,2)的对应点为A′(-7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10.
10
【解析】因为平移后点A(-1,2)的对应点为A′(-7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10. 已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为_____.
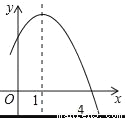
 x1=4,x2=﹣2
【解析】试题分析:由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解.
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线...
x1=4,x2=﹣2
【解析】试题分析:由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解.
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线... 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
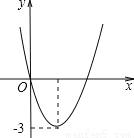
A. -3 B. 3 C. -6 D. 9
 B
【解析】先根据抛物线的开口向上可知a>0,由顶点纵坐标为-3得出b与a关系,再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式,求出m的取值范围即可.
【解析】
∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0, =-3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3...
B
【解析】先根据抛物线的开口向上可知a>0,由顶点纵坐标为-3得出b与a关系,再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式,求出m的取值范围即可.
【解析】
∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0, =-3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3... 因式分【解析】
(1)20a3﹣30a2
(2)16﹣(2a+3b)2
(3)﹣16x2y2+12xy3z
(4)5x2y﹣25x2y2+40x3y
(5)x2(a﹣b)2﹣y2(b﹣a)2
(6)(a2+b2)2﹣4a2b2
(7)18b(a﹣b)2+12(b﹣a)3
(8)x(x2+1)2﹣4x3
(9)(x2﹣2x)2﹣3(x2﹣2x)
(10)(2x﹣1)2﹣6(2x﹣1)+9
(11)16x4﹣72x2y2+81y4
(12)a5﹣a
(13)25(x+y)2﹣9(x﹣y)2
(14)m2﹣3m﹣28
(15)x2+x﹣20.
 (1)10a2(2a﹣3);(2)(4+2a+3b)(4﹣2a﹣3b);
(3)﹣4xy2(4x﹣3yz);
(4)5x2y(1﹣5y+8x);
(5)(a﹣b)2(x+y)(x﹣y);
(6)(a+b)2(a﹣b)2;
(7)6(b﹣a)2(5b﹣2a);
(8)x(x+1)2(x﹣1)2;
(9)x(x﹣2)(x﹣3)(x+1);
(10)4(x...
(1)10a2(2a﹣3);(2)(4+2a+3b)(4﹣2a﹣3b);
(3)﹣4xy2(4x﹣3yz);
(4)5x2y(1﹣5y+8x);
(5)(a﹣b)2(x+y)(x﹣y);
(6)(a+b)2(a﹣b)2;
(7)6(b﹣a)2(5b﹣2a);
(8)x(x+1)2(x﹣1)2;
(9)x(x﹣2)(x﹣3)(x+1);
(10)4(x... 5x2﹣25x2y的公因式为__.
 5x2
【解析】∵5x2﹣25x2y=5x2(1-y),
∴5x2﹣25x2y的公因式为5x2.
5x2
【解析】∵5x2﹣25x2y=5x2(1-y),
∴5x2﹣25x2y的公因式为5x2. 等腰三角形的对称轴是______.
 顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
故答案是:顶角平分线所在直线.
顶角平分线所在直线
【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,如图所示:等腰三角形的对称轴是顶角平分线所在直线.
故答案是:顶角平分线所在直线. 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20 m,高度DC=30 m,则信号发射塔顶端到地面的高度(即FG的长)为( )
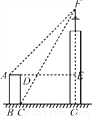
A. (35 +55)m B. (25
+55)m B. (25 +45)m C. (25
+45)m C. (25 +75)m D. (50+20
+75)m D. (50+20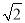 )m
)m
 C
【解析】设CG=xm,由图可以知道:EF=(x+20) ·,FG=x·,
则(x+20) ·+30= x·,
计算出x=,
则FG= x·==m,
故选C.
C
【解析】设CG=xm,由图可以知道:EF=(x+20) ·,FG=x·,
则(x+20) ·+30= x·,
计算出x=,
则FG= x·==m,
故选C. 
