题目内容
抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），这条抛物线的对称轴是（ ）
A. 直线x=1 B. 直线x= -1 C. 直线x=2 D. 直线x= -2
A
【解析】∵抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），
∴这条抛物线的对称轴是：x=，即x=1；
故选：A．
练习册系列答案
中考解读考点精练系列答案
相关题目
已知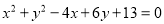
，求
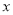和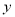
的值分别是多少？
x=2;y=-3
【解析】试题分析：运用完全平方公式把x²+y²-4x+6y+13化成(x-2)²+(y+3)²的形式即可知答案.
试题解析：由x²+y²-4x+6y+13=0 ，
得(x-2)²+(y+3)²=0，
∴x-2=0，y+3=0，
∴x=2，y=-3. 在平面直角坐标系中描出下列各点A（5，1），B（5，0），C（2，1），D（2，3），并顺次连接，且将所得图形向下平移4个单位，写出对应点A＇、B＇、C＇、D＇的坐标。
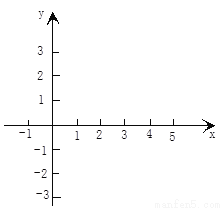
A＇（5，－3）B＇（5，－4）C＇（2，－3）D＇（2，－1）
【解析】试题分析：直接利用平移中点的变化规律求解即可．
试题解析：在平面直角坐标系中各点的位置如图所示：
由点的平移规律可知，点（x，y）向下平移4个单位后的点的坐标是（x，y-4），
∴平移后各点的坐标分别为A′（5，-3），B′（5，-4），C′（2，-3），D′（2，-1）. 抛物线y=x2-4x+m与x轴的一个交点的坐标为（1，0），则此抛物线与x轴的另一个交点的坐标是____
（3，0）
【解析】把点（1，0）代入抛物线y=x2-4x+m中，得m=3，
所以，原方程为y=x2-4x+3，
令y=0，解方程x2-4x+3=0，得x1=1，x2=3
∴抛物线与x轴的另一个交点的坐标是（3，0）．
故答案为：（3，0）． 如图，将二次函数y=31x2-999x+892的图形画在坐标平面上，判断方程31x2-999x+892=0的两根，下列叙述何者正确（ ）
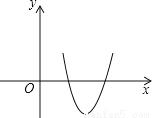
A. 两根相异，且均为正根
B. 两根相异，且只有一个正根
C. 两根相同，且为正根
D. 两根相同，且为负根
A
【解析】∵二次函数y=31x2-999x+892的图象与x轴有两个交点，且与x轴的正半轴相交，
∴方程31x2-999x+892=0有两个正实根．
故选：A． 利用分解因式计算：
（1）2022+202×196+982
（2）（﹣2）100+（﹣2）100．
（1）90000；（2）2101．
【解析】试题分析：（1）通过观察，显然符合完全平方公式，利用完全平方公式分解因式计算．
（2）利用提取公因式法进行因式分解进行计算．
【解析】
（1）原式=2022+2×202×98+982
=（202+98）2
=3002
=90000．
（2）原式=（﹣2）100×（1+1）=2101． a2﹣2ab+b2、a2﹣b2的公因式是__．
a﹣b
【解析】∵a2﹣2ab+b2=(a-b)2、a2﹣b2=(a+b)(a-b),
∴a2﹣2ab+b2、a2﹣b2的公因式是a-b. 等边三角形有_________条对称轴，矩形有__________条对称轴.
3 2
【解析】∵等腰三角形有一条对称轴，
∴等边三角形可以看成以各个点为顶点的等腰三角形，
而每一种情况下都分别有一条对称轴，
∴等边三角形有三条对称轴.
故答案为：3；2. 如图，某同学在楼房的A处测得荷塘的一端B处的俯角为30°，荷塘另一端D与点C、B在同一条直线上．已知AC＝32米，CD＝16米，则荷塘宽BD为________米(取
≈1.73，结果保留整数)．
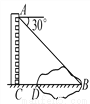
39
【解析】试题分析：根据题意可得：∠B=30°，在Rt△ABC中，tan∠B=tan30°=，则BC=32≈55米，则BD=BC-CD=55-16=39米．