��Ŀ����
��x1��x2��x1��x2���Ƿ��̣�x-a����x-b��=1��a��b��������������ʵ��x1��x2��a��b�Ĵ�С��ϵΪ��������
A. x1��x2��a��b B. x1��a��x2��b
C. x1��a��b��x2 D. a��x1��b��x2
 C
���������������������ͼ���Ƚϼ�����������x��a����x��b��=0ͼ����㻭һ�����������ϵģ���x�����������㣩��������ƽ��һ����λ�����ǣ�x��a����x��b��=1����ʱ��x��Ľ������x1��x2������ͬһ����ϵ�£��������֣����ǣ�x1��a��b��x2��
��ѡ��C��
C
���������������������ͼ���Ƚϼ�����������x��a����x��b��=0ͼ����㻭һ�����������ϵģ���x�����������㣩��������ƽ��һ����λ�����ǣ�x��a����x��b��=1����ʱ��x��Ľ������x1��x2������ͬһ����ϵ�£��������֣����ǣ�x1��a��b��x2��
��ѡ��C��
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д��ֽ���ʽ�� 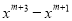 =____________________.
=____________________.
 xm+1(x+1)(x-1)
��������= xm+1(x2-1)= xm+1(x+1)(x-1)��
�ʴ�Ϊ��xm+1(x+1)(x-1).
xm+1(x+1)(x-1)
��������= xm+1(x2-1)= xm+1(x+1)(x-1)��
�ʴ�Ϊ��xm+1(x+1)(x-1). �ı���ABCD�����������ֱ�ΪA(2,4)��B(0,2)��C(2,1)��D(3,2)�����ı�������ƽ��4����λ���ȣ�������ƽ��3����λ���ȣ��õ��ı���A��B��C��D��.
(1)�ı���A��B��C��D�����ı���ABCD��Ӧ��ĺ�������ʲô��ϵ���������أ��ֱ�д��A��B��C��D������ꣻ
(2)������ı���A��B��C��D�俴�������ı���ABCD����һ��ƽ�Ƶõ��ģ���ָ����һƽ�Ƶķ���;��룮

 ������.
���������������: (1)����ͼ��,�ֱ�д���ı���A��B��C��D�����ı���ABCD����������,�Աȷ���:��Ӧ��ĺ�����ֱ����4,������ֱ����3,A��(��2,7),B��(��4,5),C��(��2,4),D��(��1,5),
(2)����AA��,���ݹ��ɶ������:AA�䣽��5.������ı���A��B��C��D�俴�������ı���ABCD����һ��ƽ�Ƶõ���,��ôƽ�Ƶķ�������A��A��ķ���,ƽ...
������.
���������������: (1)����ͼ��,�ֱ�д���ı���A��B��C��D�����ı���ABCD����������,�Աȷ���:��Ӧ��ĺ�����ֱ����4,������ֱ����3,A��(��2,7),B��(��4,5),C��(��2,4),D��(��1,5),
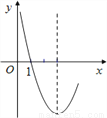
(2)����AA��,���ݹ��ɶ������:AA�䣽��5.������ı���A��B��C��D�俴�������ı���ABCD����һ��ƽ�Ƶõ���,��ôƽ�Ƶķ�������A��A��ķ���,ƽ... ��ͼ�����κ���y=x2-6x+n�IJ���ͼ����ͼ��ʾ��������x��һԪ���η���x2-6x+n=0��һ����Ϊx1=1������һ����x2= ___________.
 5��
��������������������ݶ��κ�����ͼ����x��Ľ�����ڶԳ���Գƣ�ֱ�����x2��ֵ��
�����������ͼ��֪���Գ���Ϊx=-
���ݶ��κ�����ͼ��ĶԳ��ԣ�
��ã�x2=5��
5��
��������������������ݶ��κ�����ͼ����x��Ľ�����ڶԳ���Գƣ�ֱ�����x2��ֵ��
�����������ͼ��֪���Գ���Ϊx=-
���ݶ��κ�����ͼ��ĶԳ��ԣ�
��ã�x2=5�� ��֪����y=��x-a����x-b��������a��b����ͼ����ͼ��ʾ������y=ax+b��ͼ�������ȷ���ǣ�������
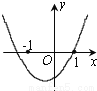
A. 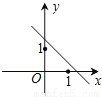 B.
B. 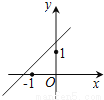 C.
C. 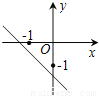 D.
D. 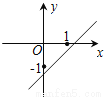
 D
������������ͼ��ɵó����̣�x-a����x-b��=0������ʵ����Ϊa��b����һ��һ���������ľ���ֵ��
��a��b����a��0��b��0��
�ຯ��y=ax+b��ͼ����һ�����������ޣ�
��ѡ��D��
D
������������ͼ��ɵó����̣�x-a����x-b��=0������ʵ����Ϊa��b����һ��һ���������ľ���ֵ��
��a��b����a��0��b��0��
�ຯ��y=ax+b��ͼ����һ�����������ޣ�
��ѡ��D�� ��ͼ����֪���κ���y��ax2��bx��c�IJ���ͼ����ͼ���֪����x��һԪ���η���ax2��bx��c��0���������ֱ���x1��1.6��x2��( )
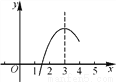
A. ��1.6 B. 3.2 C. 4.4 D. ���϶�����
 C
������������ͼ��֪�������ߵĶԳ���Ϊx=3����������������Գ�ͼ�����֪�����������x2��
��������
��������ͼ���֪��Գ���Ϊx=3��
������������Գ�ͼ��
����������x��������������x=3�Գƣ�
������x��һԪ���η���ax2+bx+c=0���������ֱ���x1��x2��
��������2��3=x1+x2��
��x1=1.6��
��x2=4.4��
...
C
������������ͼ��֪�������ߵĶԳ���Ϊx=3����������������Գ�ͼ�����֪�����������x2��
��������
��������ͼ���֪��Գ���Ϊx=3��
������������Գ�ͼ��
����������x��������������x=3�Գƣ�
������x��һԪ���η���ax2+bx+c=0���������ֱ���x1��x2��
��������2��3=x1+x2��
��x1=1.6��
��x2=4.4��
... ��x+y=1��xy=��7����x2y+xy2=__��
 ��7
����������x+y=1��xy=��7��
��x2y+xy2=xy(x+y)=-7��1=-7.
��7
����������x+y=1��xy=��7��
��x2y+xy2=xy(x+y)=-7��1=-7. ���غϵ�����ĶԳ�����_____________.
 ���������������߶εĴ�ֱƽ����
��������������֮���߶����
��������֪���غ����㣬��һ�߶�
��ԭ������һ���߶εĶԳ���
���߶εĶԳ��������Ĵ�ֱƽ����
��غϵ�����ĶԳ��������������������߶εĴ�ֱƽ����.
�ʴ�Ϊ�����������������߶εĴ�ֱƽ����
���������������߶εĴ�ֱƽ����
��������������֮���߶����
��������֪���غ����㣬��һ�߶�
��ԭ������һ���߶εĶԳ���
���߶εĶԳ��������Ĵ�ֱƽ����
��غϵ�����ĶԳ��������������������߶εĴ�ֱƽ����.
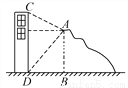
�ʴ�Ϊ�����������������߶εĴ�ֱƽ���� ��ͼ���ڸ߶���21��СɽA����ý�����CD����C��������Ϊ30�㣬�ײ�D���ĸ���Ϊ45�㣬�����������ĸ߶�CD��_________��(�����������)��
 (7����21)
�������������������AE��CD�ڵ�E����Rt��ABD�У���ADB=45�㣬��DE=AE=BD=AB=21���ף���
��Rt��AEC�У�CE=AE•tan��CAE=21��=7���ף�����CD=��21+7���ף�
(7����21)
�������������������AE��CD�ڵ�E����Rt��ABD�У���ADB=45�㣬��DE=AE=BD=AB=21���ף���
��Rt��AEC�У�CE=AE•tan��CAE=21��=7���ף�����CD=��21+7���ף� 
