如图,A、B两点的坐标分别为(2,3)、(4,1).
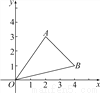
(1)求△ABO的面积;
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′,求△O′A′B′的3个顶点的坐标.
 (1)S△ABO=5;(2)A′(2,0),B′(4,-2),O′(0,-3).
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO=3×4-×3×2-×4×1-×2×2=5,
(2)A′(2,0),B′(4,-2),O′(0,-3).
(1)S△ABO=5;(2)A′(2,0),B′(4,-2),O′(0,-3).
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO=3×4-×3×2-×4×1-×2×2=5,
(2)A′(2,0),B′(4,-2),O′(0,-3). 在平面直角坐标系中,点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,则A′B′可表示为 .
 x=-1(-2≤y≤3).
【解析】
试题解析:∵点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,
∴点A′的坐标为(-1,3);点B′的坐标为(-1,-2),
∴线段A′B′可表示为 x=-1(-2≤y≤3).
x=-1(-2≤y≤3).
【解析】
试题解析:∵点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,
∴点A′的坐标为(-1,3);点B′的坐标为(-1,-2),
∴线段A′B′可表示为 x=-1(-2≤y≤3). 已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
 (1)见解析;(2)C(0,1);(3)平移规律是(x+3,y),所以A1(2,﹣2),B1(4,4),C1(3,1).
【解析】试题分析:画出平面直角坐标系后描出线段AB的中点C,根据平移的规律求出线段A1B1两个端点及线段中点C1的坐标为A1(2,﹣2),B1(4,4),C1(3,1).
试题解析:【解析】
(1)坐标系如图:
(2)C(0,1);
(3)平移规律是(...
(1)见解析;(2)C(0,1);(3)平移规律是(x+3,y),所以A1(2,﹣2),B1(4,4),C1(3,1).
【解析】试题分析:画出平面直角坐标系后描出线段AB的中点C,根据平移的规律求出线段A1B1两个端点及线段中点C1的坐标为A1(2,﹣2),B1(4,4),C1(3,1).
试题解析:【解析】
(1)坐标系如图:
(2)C(0,1);
(3)平移规律是(... 已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
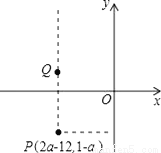
 (1)4;(2)(﹣4,1);(3)当a=2时,1﹣a=﹣1,所以PQ>1;当a=3时,1﹣a=﹣2,所以PQ>2;当a=4时,1﹣a=﹣3,所以PQ>3;当a=5时,1﹣a=﹣4,所以PQ>4.
【解析】试题分析:(1)点P的纵坐标为﹣3,即1﹣a=﹣3;解可得a的值;
(2)根据题意:由a=4得:2a﹣12=﹣4;进而根据又点Q(x,y)位于第二象限,所以y>0;取符合条件的值,可...
(1)4;(2)(﹣4,1);(3)当a=2时,1﹣a=﹣1,所以PQ>1;当a=3时,1﹣a=﹣2,所以PQ>2;当a=4时,1﹣a=﹣3,所以PQ>3;当a=5时,1﹣a=﹣4,所以PQ>4.
【解析】试题分析:(1)点P的纵坐标为﹣3,即1﹣a=﹣3;解可得a的值;
(2)根据题意:由a=4得:2a﹣12=﹣4;进而根据又点Q(x,y)位于第二象限,所以y>0;取符合条件的值,可... 下列各式中能用平方差公式分解因式的是( )
A. 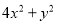 B.
B. 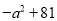 C.
C. 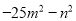 D.
D. 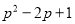
 B
【解析】A选项4x2+y2,符号相同,无法运用平方差公式分解因式,故此选项错误;B选项-a2+81,能运用平方差公式分解因式,故此选项正确;C选项-25m2-n2,符号相同,无法运用平方差公式分解因式,故此选项错误;D选项p2-2p+1,无法运用平方差公式分解因式,故此选项错误,
故选B.
B
【解析】A选项4x2+y2,符号相同,无法运用平方差公式分解因式,故此选项错误;B选项-a2+81,能运用平方差公式分解因式,故此选项正确;C选项-25m2-n2,符号相同,无法运用平方差公式分解因式,故此选项错误;D选项p2-2p+1,无法运用平方差公式分解因式,故此选项错误,
故选B. 一个多项式分解因式的结果是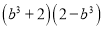 ,那么这个多项式是( )
,那么这个多项式是( )
A. 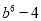 B.
B. 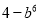 C.
C. 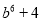 D.
D. 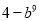
 B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B.
B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B. 下列各式中不能用平方差公式分解的是( )
A. 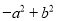 B.
B. 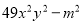 C.
C. 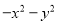 D.
D. 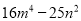
 C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C.
C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C. 不论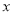 ,
, 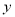 为任何实数,
为任何实数, 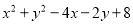 的值总是( )
的值总是( )
A. 正数 B. 负数 C. 非负数 D. 非正数
 A
【解析】x²+y²-4x-2y+8=(x²-4x+4)+(y²-2y+1)+3=(x-2)2+(y-1)2+3≥3,
不论x,y为任何实数,x²+y²-4x-2y+8的值总是大于等于3,
故选A.
A
【解析】x²+y²-4x-2y+8=(x²-4x+4)+(y²-2y+1)+3=(x-2)2+(y-1)2+3≥3,
不论x,y为任何实数,x²+y²-4x-2y+8的值总是大于等于3,
故选A. 不论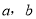 为何有理数,
为何有理数, 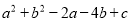 的值总是非负数,则c的最小值是( )
的值总是非负数,则c的最小值是( )
A. 4 B. 5 C. 6 D. 无法确定
 B
【解析】试题解析:∵a2+b2-2a-4b+c=(a-1)2-1+(b-2)2-4+c=(a-1)2+(b-2)2+c-5≥0,
∴c的最小值是5;
故选B.
B
【解析】试题解析:∵a2+b2-2a-4b+c=(a-1)2-1+(b-2)2-4+c=(a-1)2+(b-2)2+c-5≥0,
∴c的最小值是5;
故选B. 若非零实数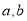 满足
满足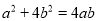 ,则
,则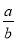 的值为( )
的值为( )
A. -2 B. 2 C. 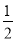 D.
D. 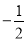
 B
【解析】试题解析:把a2+4b2=4ab,变形得:()2-4•+4=0,即(-2)2=0,
解得: =2,
故选B
B
【解析】试题解析:把a2+4b2=4ab,变形得:()2-4•+4=0,即(-2)2=0,
解得: =2,
故选B