题目内容
在平面直角坐标系中,点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,则A′B′可表示为 .
 x=-1(-2≤y≤3).
【解析】
试题解析:∵点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,
∴点A′的坐标为(-1,3);点B′的坐标为(-1,-2),
∴线段A′B′可表示为 x=-1(-2≤y≤3).
x=-1(-2≤y≤3).
【解析】
试题解析:∵点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,
∴点A′的坐标为(-1,3);点B′的坐标为(-1,-2),
∴线段A′B′可表示为 x=-1(-2≤y≤3).
练习册系列答案
相关题目
已知,在?ABCD中,BC-AB=2cm,BC=4cm,则?ABCD的周长是( )
A.6cm B.12cm C.8cm D.10cm
 B.
【解析】
试题解析:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,
∵BC-AB=2cm,BC=4cm,
∴AB=DC=2cm,
∴?ABCD的周长是=2+2+4+4=12cm.
故选B.
B.
【解析】
试题解析:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,
∵BC-AB=2cm,BC=4cm,
∴AB=DC=2cm,
∴?ABCD的周长是=2+2+4+4=12cm.
故选B. 如果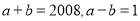 ,那么
,那么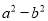 =___________.
=___________.
 2008
【解析】试题解析:∵a2-b2=(a+b)(a-b),
∴把a+b=2008,a-b=1代入上式得:
原式=2008×1=2008.
故答案为:2008.
2008
【解析】试题解析:∵a2-b2=(a+b)(a-b),
∴把a+b=2008,a-b=1代入上式得:
原式=2008×1=2008.
故答案为:2008. 若a、b、c是△ABC的三边,满足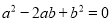 且
且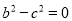 ,则△ABC的形状是( )
,则△ABC的形状是( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等边三角形
 D
【解析】∵a2-2ab+b2=0且b2-c2=0,∴(a-b)2=0且(b+c)(b-c)=0,
∴a=b且b=c,即a=b=c,∴△ABC为等边三角形,
故选D.
D
【解析】∵a2-2ab+b2=0且b2-c2=0,∴(a-b)2=0且(b+c)(b-c)=0,
∴a=b且b=c,即a=b=c,∴△ABC为等边三角形,
故选D. 下列各式中不能用平方差公式分解的是( )
A. 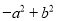 B.
B. 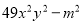 C.
C. 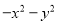 D.
D. 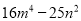
 C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C.
C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C. 在平面直角坐标系中,将图形沿x轴正方向平移3个单位,变化前后对应点 纵坐标不变, 横坐标增加3个单位.
 纵;横
【解析】
试题分析:图形沿x轴正方向平移,改变的是y值,x值不变。
纵;横
【解析】
试题分析:图形沿x轴正方向平移,改变的是y值,x值不变。 如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点P′(x0+5,y0-2).
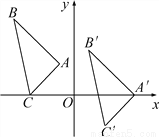
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为6.
 (1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△AB...
(1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△AB... 如图,抛物线y= -x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y____0(填“>”“=”或“<”号).

 <
【解析】试题分析:根据题意可得函数的对称轴为x=1,∵0<<1,则1<<2,∴x=-2<0,根据图象可得:当x<0时,y<0.
<
【解析】试题分析:根据题意可得函数的对称轴为x=1,∵0<<1,则1<<2,∴x=-2<0,根据图象可得:当x<0时,y<0. 已知M、N是线段AB的垂直平分线上任意两点,则∠MAN和∠MBN之间关系是____.
 ∠MAN=∠MBN
【解析】∵原题当中没有说明点M、N在线段AB的位置,
∴可能有以下四种情况:
①如图①,点M、N在线段AB两侧时,
∵M、N是线段AB的垂直平分线上任意两点,
∴点A、B两点关于直线MN轴对称,
∴线段MA、MB两点关于直线MN轴对称,
同理线段NA、NB两点关于直线MN轴对称,
∴△MAN与△MBN关于直线MN轴对称,
∴...
∠MAN=∠MBN
【解析】∵原题当中没有说明点M、N在线段AB的位置,
∴可能有以下四种情况:
①如图①,点M、N在线段AB两侧时,
∵M、N是线段AB的垂直平分线上任意两点,
∴点A、B两点关于直线MN轴对称,
∴线段MA、MB两点关于直线MN轴对称,
同理线段NA、NB两点关于直线MN轴对称,
∴△MAN与△MBN关于直线MN轴对称,
∴... 
