题目内容
不论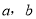
为何有理数, 
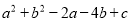的值总是非负数,则c的最小值是( )
A. 4 B. 5 C. 6 D. 无法确定
B
【解析】试题解析：∵a2+b2-2a-4b+c=（a-1）2-1+（b-2）2-4+c=（a-1）2+（b-2）2+c-5≥0，
∴c的最小值是5；
故选B．
练习册系列答案
相关题目
如图，BD是?ABCD的对角线，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F．
（1）补全图形，并标上相应的字母；
（2）求证：AE=CF．
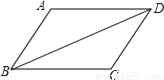
(1)作图见解析；（2）证明见解析.
【解析】试题分析：（1）根据题意画出图形即可；
（2）由平行四边形的性质得出△ABD的面积=△BCD的面积，得出BD•AE=BD•CF，即可得出结论．
试题解析：（1）如图所示：
（2）∵四边形ABCD是平行四边形，∴△ABD的面积=△BCD的面积，∴BD•AE=BD•CF，∴AE=CF． 下列说法中正确的是（ ）
A. 能重合的图形一定是成轴对称图形
B. 成中心对称的图形一定是重合的图形
C. 两个成中心对称的图形的对称点连线不一定过对称中心
D. 两个会重合的三角形一定关于某一点成中心对称
B
【解析】试题解析：轴对称图形是沿对称轴折叠重合的图形，而全等的图形即可重合，所以A错误；
中心对称的图形全等即可重合，所以B正确；
成中心对称的图形的对称点连线一定过对称中心，所以C错误；
全等的三角形关于某一点旋转180°后可以重合，才是成中心对称的．所以D错误.
故选B. 分解因式：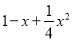 
=____________________.
【解析】1-x+x2=-x+1=( -1)2，
故答案为： . 若a、b、c是△ABC的三边，满足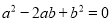
且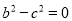
，则△ABC的形状是（ ）
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等边三角形
D
【解析】∵a2-2ab+b2=0且b2-c2=0，∴（a-b）2=0且（b+c）（b-c）=0，
∴a=b且b=c，即a=b=c，∴△ABC为等边三角形，
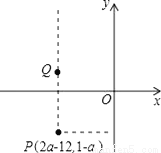
故选D． 已知点P（2a﹣12，1﹣a）位于第三象限，点Q（x，y）位于第二象限且是由点P向上平移一定单位长度得到的．
（1）若点P的纵坐标为﹣3，试求出a的值；
（2）在（1）题的条件下，试求出符合条件的一个点Q的坐标；
（3）若点P的横、纵坐标都是整数，试求出a的值以及线段PQ长度的取值范围．
（1）4；（2）（﹣4，1）；（3）当a=2时，1﹣a=﹣1，所以PQ＞1；当a=3时，1﹣a=﹣2，所以PQ＞2；当a=4时，1﹣a=﹣3，所以PQ＞3；当a=5时，1﹣a=﹣4，所以PQ＞4．
【解析】试题分析：（1）点P的纵坐标为﹣3，即1﹣a=﹣3；解可得a的值；
（2）根据题意：由a=4得：2a﹣12=﹣4；进而根据又点Q（x，y）位于第二象限，所以y＞0；取符合条件的值，可... 在平面直角坐标系中，将图形沿x轴正方向平移3个单位，变化前后对应点 纵坐标不变， 横坐标增加3个单位．
纵；横
【解析】
试题分析：图形沿x轴正方向平移，改变的是y值，x值不变。 如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（ ）
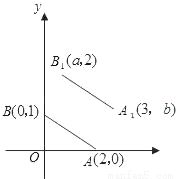
A. 2 B. 3 C. 4 D. 5
A
【解析】由B点平移前后的纵坐标分别为1,2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2,3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2,故选:A. 将多项式-6a3b2-3a2b2+12a2b3分解因式时，应提取的公因式是（ ）
A．-3a2b2 B．-3ab C．-3a2b D．-3a3b3
A
【解析】
在找公因式时，一找系数的最大公约数，二找相同字母的最低次幂．同时注意首项系数通常要变成正数．