如图，在?ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则阴影部分的面积为( )
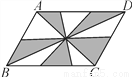
A. 3 B. 6 C. 12 D. 24
C
【解析】∵四边形ABCD为平行四边形，∴OA=OC，OB=OD，
∴△OBE≌△ODH，△OAQ≌△OCG，△OPD≌△OFB，∴S阴影=S△BCD，
∴S△BCD=S平行四边形ABCD=×6×4=12．故选C. 已知，在?ABCD中，BC-AB=2cm，BC=4cm，则?ABCD的周长是（ ）
A．6cm B．12cm C．8cm D．10cm
B.
【解析】
试题解析：∵四边形ABCD是平行四边形，
∴AB=CD，BC=AD，
∵BC-AB=2cm，BC=4cm，
∴AB=DC=2cm，
∴?ABCD的周长是=2+2+4+4=12cm．
故选B． 如图，在?ABCD中，M是BC延长线上的一点，若∠A＝135°，则∠MCD的度数是( )
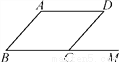
A. 45° B. 55° C. 65° D. 75°
A
【解析】根据平行四边形的邻角互补，因为∠A＝135°，所以 ,又因为 ,所以 .
故选A. 如图，在?ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于
EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（ ）
A. AG平分∠DAB B. AD=DH C. DH=BC D. CH=DH
D
【解析】试题分析：由角平分线的作法，依题意可知AG平分∠DAB，A正确；∠DAH＝∠BAH，又AB∥DC，所以∠BAH＝∠ADH，所以，∠DAH＝∠ADH，所以，AD＝DH，又AD＝BC，所以，DH＝BC，B、C正确，故答案选D. 如图，在?ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数为__．
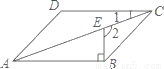
110°.
【解析】根据平行四边形的性质可得AB∥CD，根据平行线的性质可得∠1=∠CAB=20°，因BE⊥AB，可得∠EBA=90°，所以∠2=∠EBA+∠CAB=90°+20°=110°. 如图所示，已知在平行四边形ABCD中，BE=DF．求证：AE=CF．
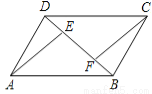
证明：∵BE=DF，
∴BE-EF=DF-EF，
∴DE=BF，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴∠ADE=∠CBF，
在△ADE和△CBF中，
∴△ADE≌△CBF（SAS），
∴AE=CF．
【解析】
求出DE=BF，根据平行四边形性质求出AD=BC，AD∥BC，推出∠ADE=∠CBF，证出△ADE≌△CBF即可． 已知：如图，四边形ABCD是平行四边形，延长BA至点E，使AE+CD=AD．连结CE，求证：CE平分∠BCD．
证明见解析．
【解析】试题分析：由平行四边形的性质得出AB∥CD，AB=CD，AD=BC，由平行线的性质得出∠E=∠DCE，由已知条件得出BE=BC，由等腰三角形的性质得出∠E=∠BCE，得出∠DCE=∠BCE即可．
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，AD=BC，∴∠E=∠DCE，∵AE+CD=AD，∴BE=BC，∴∠E=∠BCE，∴∠DCE=∠BCE，... 已知?ABCD的周长为36cm，过点A作AE⊥BC，AF⊥CD，垂足分别为E、F.若AE＝2cm，AF＝4cm.求?ABCD的各边长．
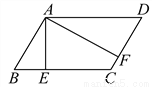
AB＝CD＝6cm，AD＝BC＝12cm.
【解析】【试题分析】根据?ABCD的周长为36cm，得BC＋CD＝18；根据等面积法，得S?ABCD＝BC·AE＝CD·AF，解得：BC＝2CD，两式联立方程组，，解得，根据平行四边形的对边相等，得AB＝CD＝6cm，AD＝BC＝12cm.
【试题解析】
∵?ABCD中，AB＝CD，BC＝AD，又∵?ABCD的周长为36cm.即AB＋B... 如图，BD是?ABCD的对角线，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F．
（1）补全图形，并标上相应的字母；
（2）求证：AE=CF．
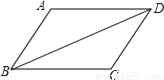
(1)作图见解析；（2）证明见解析.
【解析】试题分析：（1）根据题意画出图形即可；
（2）由平行四边形的性质得出△ABD的面积=△BCD的面积，得出BD•AE=BD•CF，即可得出结论．
试题解析：（1）如图所示：
（2）∵四边形ABCD是平行四边形，∴△ABD的面积=△BCD的面积，∴BD•AE=BD•CF，∴AE=CF． 如图，E是?ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
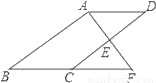
（1）证明过程见解析；（2）8.
【解析】试题分析：（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD，
...