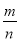题目内容
已知，在?ABCD中，BC-AB=2cm，BC=4cm，则?ABCD的周长是（ ）
A．6cm B．12cm C．8cm D．10cm
B.
【解析】
试题解析：∵四边形ABCD是平行四边形，
∴AB=CD，BC=AD，
∵BC-AB=2cm，BC=4cm，
∴AB=DC=2cm，
∴?ABCD的周长是=2+2+4+4=12cm．
故选B．
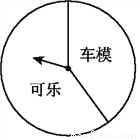
轻松暑假总复习系列答案某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
（1）472，0.596；（2）0.6，0.6；（3）144°.
【解析】试题分析: 在同样条件下,做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率,
（1）当试验的可能结果不是有限个,或各种结果发生的可能性不相等时,一般用统计频率的方法来估计概率,
（2）利用频率估计概率的数学依据是大数定律:当试验次数很大时,随机事件A出现的频率,稳定... 掷一枚正方体的骰子，各个面上分别标有数字1， 2，3，4，5，6，求下列事件发生的频率的大小：
①朝上的数字是奇数；
②朝上的数字能被3除余1；
③朝上的数字不是3的倍数；
④朝上的数字小于6；
⑤朝上的数字不小于3.
①；②；③；④；⑤
【解析】试题分析:本题考察可能性大小的应用，关键是推断出各色扑克被抽到的频率是多少.
①【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，每一个点数出现的频率相同.其中，是奇数点的有3种可能，故其频率是；
②【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，... 下列说法正确的是( )
A. 如果一件事情发生的可能性达到99.9999%，说明这件事必然发生；
B. 如果一事件不是不可能事件,说明此事件是不确定事件；
C. 可能性的大小与不确定事件有关；
D. 如果一事件发生的可能性为百万分之一，那么这事件是不可能事件.
C
【解析】试题分析：根据必然事件、不可能事件、不确定事件的概念依次分析即可.
A.如果一件事情发生的可能性达到99.9999%,说明这件事很可能发生，但仍然是不确定事件，故错误；
B.如果一事件不是不可能事件,说明此事件是不确定事件或必然事件，故错误；
C.可能性的大小与不确定事件有关，正确；
D.如果一事件发生的可能性为百万分之一，这事件是不确定事件，故错误；
... 已知：如图，四边形ABCD是平行四边形，延长BA至点E，使AE+CD=AD．连结CE，求证：CE平分∠BCD．
证明见解析．
【解析】试题分析：由平行四边形的性质得出AB∥CD，AB=CD，AD=BC，由平行线的性质得出∠E=∠DCE，由已知条件得出BE=BC，由等腰三角形的性质得出∠E=∠BCE，得出∠DCE=∠BCE即可．
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，AD=BC，∴∠E=∠DCE，∵AE+CD=AD，∴BE=BC，∴∠E=∠BCE，∴∠DCE=∠BCE，... 线段垂直平分线上的点到这条线段两个端点的距离____.
相等
【解析】根据线段垂直平分线的性质可得：线段垂直平分线上的点到这条线段两个端点的距离相等.
故答案是：相等. 如图，在锐角三角形ABC中，∠BAC＝60°，边AC、AB的垂直平分线交于点O，交AC、AB于点D、E，则∠BOC等于____.
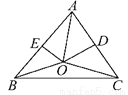
120°
【解析】∵AB,AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠OAB=∠OBA,∠OAC=∠OCA
∴∠OAB+∠OAC=∠OBA+∠OCA=∠A=60°
∴∠OBC+∠OCB=180°-2*60°=60°
∴∠BOC=180°-60°=120°.
故答案是：120°. 正方形既是_________图形，又是_____________图形
轴对称 中心对称
【解析】正方形既是轴对称图形又是中心对称图形.
故答案：轴对称，中心对称. 在平面直角坐标系中，点A的坐标是（2，3），点B的坐标是（2，-2），若把线段AB向左平移3个单位后变为A′B′，则A′B′可表示为 ．
x=-1（-2≤y≤3）．
【解析】
试题解析：∵点A的坐标是（2，3），点B的坐标是（2，-2），若把线段AB向左平移3个单位后变为A′B′，
∴点A′的坐标为（-1，3）；点B′的坐标为（-1，-2），
∴线段A′B′可表示为 x=-1（-2≤y≤3）．