题目内容
如图所示,已知在平行四边形ABCD中,BE=DF.求证:AE=CF.
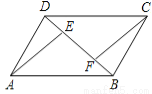
 证明:∵BE=DF,
∴BE-EF=DF-EF,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴AE=CF.
【解析】
求出DE=BF,根据平行四边形性质求出AD=BC,AD∥BC,推出∠ADE=∠CBF,证出△ADE≌△CBF即可.
证明:∵BE=DF,
∴BE-EF=DF-EF,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴AE=CF.
【解析】
求出DE=BF,根据平行四边形性质求出AD=BC,AD∥BC,推出∠ADE=∠CBF,证出△ADE≌△CBF即可.
练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
计算: 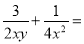 ________.
________.
 【解析】试题分析:原式=
=.
故答案为: .
【解析】试题分析:原式=
=.
故答案为: . 掷一枚质地均匀的骰子,看落地后朝上的面的点数.
(1)会出现哪些可能的结果?
(2)掷出的点数为1与掷出的点数为2的频率相同吗?掷出的点数为1与掷出的点数为3的频率相同吗?
(3)每种结果出现的频率相同吗?
 (1)可能出现朝上的面的点数是:1,2,3,4,5,6;(2)掷出的点数为1与掷出的点数为2的频率相同;掷出的点数为1与掷出的点数为3的频率相同;(3)每种结果出现的频率相同
【解析】试题分析: 掷一个质地均匀的骰子,有6种等可能的结果,每个数字的频率都稳定在 ,所以每种结果出现的可能性都相同.
(1)【解析】
掷一枚质地均匀的骰子,由于有六个面,所以落地后,可能出现朝上的面的点数是...
(1)可能出现朝上的面的点数是:1,2,3,4,5,6;(2)掷出的点数为1与掷出的点数为2的频率相同;掷出的点数为1与掷出的点数为3的频率相同;(3)每种结果出现的频率相同
【解析】试题分析: 掷一个质地均匀的骰子,有6种等可能的结果,每个数字的频率都稳定在 ,所以每种结果出现的可能性都相同.
(1)【解析】
掷一枚质地均匀的骰子,由于有六个面,所以落地后,可能出现朝上的面的点数是... 下列事件发生的可能性为0的是( )
A. 掷两枚骰子,同时出现数字“6”朝上
B. 小明从家里到学校用了10分钟,从学校回到家里却用了15分钟
C. 今天是星期天,昨天必定是星期六
D. 小明步行的速度是每小时40千米
 D
【解析】对于A,掷两枚骰子,同时出现数字“6”朝上,可能性为;
对于B,小明从家里到学校用了10分钟,从学校回到家里却用了15分钟是可能是,比如去学校时下坡,则回家时上坡,当然回家比去学校用时多;
对于C,今天是星期天,昨天必定是星期六这是一个必然发生的事件,可能性为1;
对于D,小明步行的速度是每小时40千米,是不存在的.一般人步行的速度为3-5公里每小时,所以D发生...
D
【解析】对于A,掷两枚骰子,同时出现数字“6”朝上,可能性为;
对于B,小明从家里到学校用了10分钟,从学校回到家里却用了15分钟是可能是,比如去学校时下坡,则回家时上坡,当然回家比去学校用时多;
对于C,今天是星期天,昨天必定是星期六这是一个必然发生的事件,可能性为1;
对于D,小明步行的速度是每小时40千米,是不存在的.一般人步行的速度为3-5公里每小时,所以D发生... 某单位要在两名射击队员中推出一名参加比赛,已知同等条件下,甲射中某物的可能性大于乙,则所推出的人中应( )
A. 选甲 B. 选乙 C. 都可以 D. 不能确定
 A
【解析】根据题意可知,同等条件下,甲射中某物的可能性大于乙.故应该派甲去.
故选A.
A
【解析】根据题意可知,同等条件下,甲射中某物的可能性大于乙.故应该派甲去.
故选A. 如图,在?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
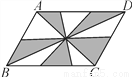
A. 3 B. 6 C. 12 D. 24
 C
【解析】∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,
∴△OBE≌△ODH,△OAQ≌△OCG,△OPD≌△OFB,∴S阴影=S△BCD,
∴S△BCD=S平行四边形ABCD=×6×4=12.故选C.
C
【解析】∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,
∴△OBE≌△ODH,△OAQ≌△OCG,△OPD≌△OFB,∴S阴影=S△BCD,
∴S△BCD=S平行四边形ABCD=×6×4=12.故选C. 如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.
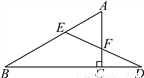
 见解析
【解析】试题分析:过E作EG垂直于AC,交AC于G,可得出EG∥BD故∠AEG=∠B,∠D=∠DEG.再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D,根据ASA定理得出△AEG≌△FEG,进而可得出结论.
试题解析:
证明:如图所示:
过E作EG垂直于AC,交AC于G,
∵∠ACB=90°,
∴EG∥BD,
∴∠AEG=∠B,∠D=∠DEG.
∵...
见解析
【解析】试题分析:过E作EG垂直于AC,交AC于G,可得出EG∥BD故∠AEG=∠B,∠D=∠DEG.再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D,根据ASA定理得出△AEG≌△FEG,进而可得出结论.
试题解析:
证明:如图所示:
过E作EG垂直于AC,交AC于G,
∵∠ACB=90°,
∴EG∥BD,
∴∠AEG=∠B,∠D=∠DEG.
∵... 判断对错:两个会重合的图形一定是中心对称图形; ___________
 错
【解析】两个会重合的图形不一定是中心对称图形,因为还要看是否存在对称中心.
故答案:错.
错
【解析】两个会重合的图形不一定是中心对称图形,因为还要看是否存在对称中心.
故答案:错. 一个多项式分解因式的结果是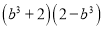 ,那么这个多项式是( )
,那么这个多项式是( )
A. 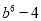 B.
B. 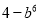 C.
C. 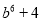 D.
D. 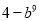
 B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B.
B
【解析】试题解析:(b3+2)(2-b3)=4-b6.
故选B. 
