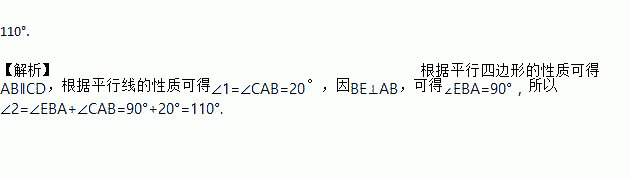题目内容
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为__.
 110°.
【解析】根据平行四边形的性质可得AB∥CD,根据平行线的性质可得∠1=∠CAB=20°,因BE⊥AB,可得∠EBA=90°,所以∠2=∠EBA+∠CAB=90°+20°=110°.
110°.
【解析】根据平行四边形的性质可得AB∥CD,根据平行线的性质可得∠1=∠CAB=20°,因BE⊥AB,可得∠EBA=90°,所以∠2=∠EBA+∠CAB=90°+20°=110°.
练习册系列答案
相关题目
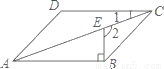
分式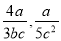 的最简公分母是_________.
的最简公分母是_________.
 15bc2
【解析】试题分析:分式与的最简公分母是15bc2.
故答案为:15bc2.
15bc2
【解析】试题分析:分式与的最简公分母是15bc2.
故答案为:15bc2. 我会连.(任意摸出一个球,可能是什么颜色?)



一定是白球 可能是白球 不可能是白球
 【解析】试题分析: 本题考察对可能性大小的应用,关键是推断出各袋子中能摸出的球的颜色的频率如何.
【解析】
因为三个袋子中所装的球的颜色是不同的,第一个袋子中全是黑球,第二是全是白球,第三个里面有黑球也有白球,所以,从第二个袋子中摸出的一定是白球,第一个袋子中摸出来的一定不是白球;第三个袋子中摸出来的可能是白球也可能是黑球.故连接如上图所示.
【解析】试题分析: 本题考察对可能性大小的应用,关键是推断出各袋子中能摸出的球的颜色的频率如何.
【解析】
因为三个袋子中所装的球的颜色是不同的,第一个袋子中全是黑球,第二是全是白球,第三个里面有黑球也有白球,所以,从第二个袋子中摸出的一定是白球,第一个袋子中摸出来的一定不是白球;第三个袋子中摸出来的可能是白球也可能是黑球.故连接如上图所示. 一个口袋里有5个红球,3个黄球,2个绿球,任意摸一个,摸( )的可能性最小.
A. 红球 B. 黄球 C. 绿球 D. 以上都不对
 C
【解析】由题意知这个口袋中装有5个红球,3个黄球,2个绿球,共有5+3+2=10个球,摸到红球的概率是,摸到黄球的概率是,摸到绿球的概率是,因此,摸到绿球的可能性最小.
故选C.
C
【解析】由题意知这个口袋中装有5个红球,3个黄球,2个绿球,共有5+3+2=10个球,摸到红球的概率是,摸到黄球的概率是,摸到绿球的概率是,因此,摸到绿球的可能性最小.
故选C. 如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
 (1)证明过程见解析;(2)8.
【解析】试题分析:(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AD∥BC,AB∥CD,
...
(1)证明过程见解析;(2)8.
【解析】试题分析:(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AD∥BC,AB∥CD,
... 如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
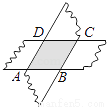
 菱形
【解析】试题分析:首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的等积转换可得邻边相等,则四边形ABCD为菱形.所以根据菱形的性质进行判断.
【解析】
过点D分别作AB,BC边上的高为AE,AF,
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边...
菱形
【解析】试题分析:首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的等积转换可得邻边相等,则四边形ABCD为菱形.所以根据菱形的性质进行判断.
【解析】
过点D分别作AB,BC边上的高为AE,AF,
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边... 如图,点D在BC上,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF.求证:AD垂直平分EF.
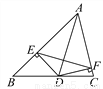
 见解析
【解析】试题分析:根据直角三角形的判定定理证明Rt△AED≌Rt△AFD,得到AE=AF,根据线段垂直平分线的判定定理证明结论.
试题解析:
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
又∵DE=DF,
∴AD是EF的垂直平分线,即AD垂直平分EF.
见解析
【解析】试题分析:根据直角三角形的判定定理证明Rt△AED≌Rt△AFD,得到AE=AF,根据线段垂直平分线的判定定理证明结论.
试题解析:
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
又∵DE=DF,
∴AD是EF的垂直平分线,即AD垂直平分EF. 关于点O成中心对称的两个四边形ABCD和DEFG,AD、BE、CF、DG都过______
 点O
【解析】对应点的连线经过对称中心.
故答案:点O.
点O
【解析】对应点的连线经过对称中心.
故答案:点O. 下列各式中能用平方差公式分解因式的是( )
A. 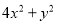 B.
B. 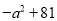 C.
C. 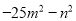 D.
D. 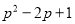
 B
【解析】A选项4x2+y2,符号相同,无法运用平方差公式分解因式,故此选项错误;B选项-a2+81,能运用平方差公式分解因式,故此选项正确;C选项-25m2-n2,符号相同,无法运用平方差公式分解因式,故此选项错误;D选项p2-2p+1,无法运用平方差公式分解因式,故此选项错误,
故选B.
B
【解析】A选项4x2+y2,符号相同,无法运用平方差公式分解因式,故此选项错误;B选项-a2+81,能运用平方差公式分解因式,故此选项正确;C选项-25m2-n2,符号相同,无法运用平方差公式分解因式,故此选项错误;D选项p2-2p+1,无法运用平方差公式分解因式,故此选项错误,
故选B.